Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 10.2 - Ex. 1
Nos Exercícios 1-6, encontre a fórmula para a n-ésima soma parcial de cada série e use-a para encontrar a soma da série se ela convergir.
Passo 1
Fala galerinha tranquilidade, essa segunda parte do capítulo se preocupa com a séries, e esses 6 primeiros problemas são para determinar qual a expressão que forma a série, isso não tem muita técnica, temos que avaliar o comportamento dela e ir tentanto, porém a convergência o divergência podemos usar a seguinte definição:
Passo 2
A formação da série pode ser dada por:
Passo 3
Enquanto a divergência pode ser calculada verificando o limite da definição:
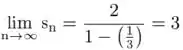
Resposta
A série converge
Exercícios de Livros Relacionados
Utilize (3) com n = 10 para dar uma estimativa melhorada da soma.
Mostre que, se queremos aproximar a soma da série ∑ n = 1 ∞ n - 1 , 001 de maneira que o erro seja menor que 5 na nona casa decimal, então precisamos somar mais que 10 11301 termos!
Estime ∑ n = 1 ∞ 2 n + 1 - 6 com precisão de cinco casas decimais.
Calcule a soma da série ∑ n = 1 ∞ 1 / n 5 com precisão de três casas decimais.
Se ∑ a n for divergente e c ≠ 0 , mostre que ∑ c a n é divergente.