Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.2 - Ex. 6
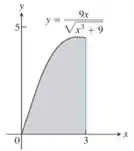
Nos Exercícios 1-6, use o método da casca para determinar os volumes dos sólidos obtidos com a rotação das regiões sombreadas em torno dos eixos indicados.
Passo 1
Lembrando do método da casca que é um método para calcular o volume de uma região segundo a fórmula:
Como o volume é em torno de , o raio da casca é igual a . Já a altura da casca é igual a . Assim,
Passo 2
Vamos fazer uma mudança de variável:
Derivando dos dois lados:
Transformando os limites inferior e superior:
Colocando na integral:
Calculando a integral:
Resposta
Exercícios de Livros Relacionados
Ache o volume do sólido gerado pela rotação, em torno da reta x = 2 , da região limitada pelo gráfico de y = 2 x - 1 6 x 3 , pelo eixo x e pela reta x = 2 .
Ache o volume do sólido gerado pela rotação, em torno do eixo y , da região limitada pelo gráfico de y = 2 x - 1 6 x 3 , pelo eixo x e pela reta x = 2 .
1 – 12. Resolva os Exercícios de 5 a 16 da seção 6.1 pelo método do invólucro cilíndrico.Nos Exercícios, ache o volume do sólido de revolução gerado pela rotação, em torno da reta indicada, da região
1 – 12. Resolva os Exercícios de 5 a 16 da seção 6.1 pelo método do invólucro cilíndrico.Nos Exercícios, ache o volume do sólido de revolução descrito quando a região dada da figura for rotacionada em
1 – 12. Resolva os Exercícios de 5 a 16 da seção 6.1 pelo método do invólucro cilíndrico.Nos Exercícios, ache o volume do sólido de revolução descrito quando a região dada da figura for rotacionada em