Enunciado
Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.3 - Ex. 24
Nos exercícios de 17 a 26, ache a equação da hipérbole satisfazendo as condições dadas e faça um esboço do gráfico.
24. Focos em e e passando pelo ponto
Passo 1
Para resolver este tipo de questão devemos conhecer a equação de uma hipérbole e onde está o seu eixo principal. A partir daí, podemos utilizar das informações dada no enunciado e de algumas relações básicas que envolvem hipérboles.
Passo 2
Como ele fala os focos da hipérbole, a partir dele e do ponto informado temos que o eixo principal está no eixo y e o centro da mesma encontra-se em Sendo assim, a equação da hipérbole em questão é dada por:
Passo 3
Como o número de unidades no comprimento do eixo transverso é , vem que . Sabemos também, que para uma hipérbole podemos escrever a seguinte relação:
Para uma hipérbole temos que . Então, , .
Sendo assim, temos que a equação da hipérbole é:
Passo 4
Um esboço do gráfico da hipérbole dada é:
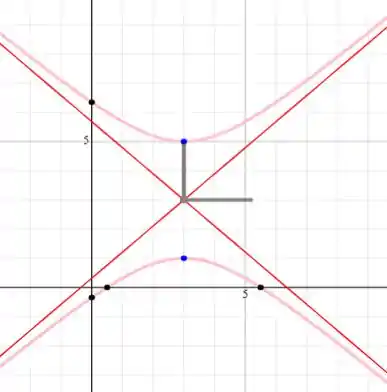
Resposta
