Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 6.6 - Ex. 18
Nos exercícios 18 a 24, representar geometricamente o campo gradiente definido pela função dada:
18.
Passo 1
Então pessoal, calcular o gradiente de um campo escalar quando temos uma função bem definidinha, assim como é o nosso caso, é bem tranquilo, tá? Basta derivarmos parcialmente em relação a cada eixo e botar tudo numa soma, desse jeito aqui ó:
Sendo assim, só precisamos encontrar essas derivadas e substituir em seus devidos lugares, ok? Então let’s go!
Passo 2
Para a derivada parcial será:
Para a derivada parcial será:
Para a derivada parcial será:
Dessa forma, nosso gradiente será:
Passo 3
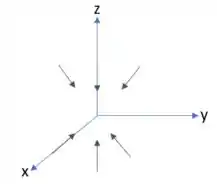
O gradiente de uma função é um vetor que aponta o sentido e a direção de maior incremento possível em um campo escalar. Se esboçarmos esse gradiente graficamente, teremos algo parecido com o seguinte:
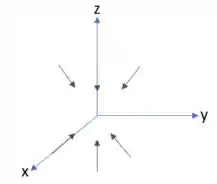
E está aí nosso resultado, galera!
Resposta
