Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.4 - Ex. 36

Nos Exercícios de 21 a 36, use o método desta secção para calcular a área da região dada; use retângulos inscritos ou circunscritos, conforme inficado. Para cada exercício, faça uma figura mostrando a região e o i-ésimo retângulo.

36. A região do exercício 35; retângulos inscritos.

Passo 1

A região do exercício é:

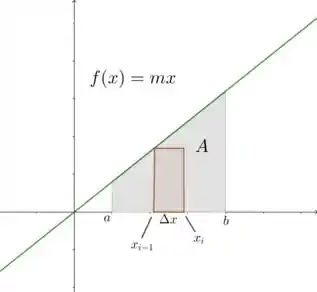
A região e o i-ésimo retângulo inscrito estão na figura.

Passo 2

Vamos calcular a área do intervalo [ a ,   b ] .

Δ x = b - a n

f x i - 1 = m a + ( i - 1 ) b - a n = m a + i b - a n - b - a n

A = lim n → + ∞ ⁡ ∑ i = 1 n f ( x i - 1 ) Δ x = lim n → + ∞ ⁡ ∑ i = 1 n m a + i b - a n - b - a n b - a n  

A = lim n → + ∞ ⁡ b - a n ∑ i = 1 n m i b - a n + a n - b + a n  

A = lim n → + ∞ ⁡ m b - a n 2 ∑ i = 1 n i b - a + a n - b + a  

A = lim n → + ∞ ⁡ m b - a n 2 b - a ∑ i = 1 n i + a n - b + a ∑ i = 1 n 1

Passo 3

Agora vamos usar as fórmulas dos somatórios e calcular o limite.

∑ i = 1 n 1 ⏞ I = n                                 ∑ i = 1 n i ⏞ = I I n ( n + 1 ) 2

A = lim n → + ∞ ⁡ m b - a n 2 b - a n ( n + 1 ) 2 + a n - b + a n

A = lim n → + ∞ ⁡ m ( b - a ) b - a n n 1 + 1 n 2 + a n n - b n + a n n n

A = m ( b - a ) b - a 1 + 0 2 + a - 0 + 0

A = m ( b - a ) b - a + 2 a 2

A = m ( b - a ) b + a 2

A = m b 2 - a 2 2     u . a

Logo, a área A é m ⁡ b 2 - a 2 2     u . a .

Resposta

A = m ⁡ b 2 - a 2 2     u . a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) Faça o gráfico da função f x = e - x 2 ,- 2 ≤ x ≤ 2 .(b) Estime a área sob o gráfico de f usando quatro retângulos aproximantes e tomando como pontos amostrais (i) as extremidades direitas e (ii)
(a) Use seis retângulos para achar estimativas de cada tipo para a área sob o gráfico dado f de de x = 0 até x = 12 . (i) L 6 (pontos amostrais estão nas extremidades esquerdas) (ii) R 6 (pontos amost
Alguns sistemas de computação algébrica têm comandos que traçam retângulos aproximantes e calculam as somas de suas áreas, pelo menos se x i * for uma extremidade esquerda ou direita. (Por exemplo, no
Com uma calculadora programável (ou um computador), é possível calcular as expressões para a soma das áreas de retângulos aproximantes, mesmo para valores grandes de n , usando l a ç o s ç . (Numa T I
(a) Estime a área sob o gráfico de f x = 1 + x ² ²de x = - 1 até x = 2 usando três retângulos aproximantes e extremidades direitas. Então, aperfeiçoe sua estimativa utilizando seis retângulos aproxima