Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.6 - Ex. 7
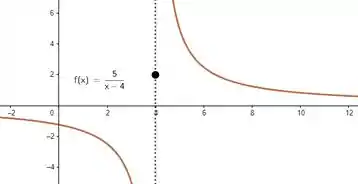
Nos exercícios de a , faça um esboço do gráfico da função; então, observando onde há quebras no gráfico, determine os valores da variável independente nos quais a função é descontínua e mostre por que a Definição não é satisfeita em cada descontinuidade
Passo 1
Bem, pra começar, vamos notar uma coisa importante no denominador da lei de formação dessa função definida por partes: ele zera quando ! Perceba que se fizermos os limites:
Chegamos a uma conclusão que nos diz tudo sobre esse carinha aí: o limite não exite! Então apesar de estar definido de tal forma que , o limite não existe e logo essa função não será contínua em
Passo 2
Pra esboçar essa função a gente lembra do resultado dos limites encontrados no passo anterior e faz ainda o limite:
Assim dá pra notar direitinho que um bom esboço seria algo parecido com essa curva simpática:
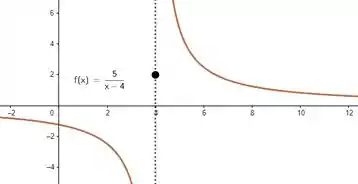
O ponto preto representa incluso na definição de .
Resposta
A função não é contínua em . O limite não existe.
