Dê exemplo de duas funções e que não são contínuas no ponto e tais que é contínua neste ponto. Faça o gráfico das funções , e .
Passo 1
Vamos dar o exemplo das funções:
Elas não são contínuas em pois os limites e não existem, os limites pela direita e pela esquerda de cada função dão resultados diferentes.
E para temos:
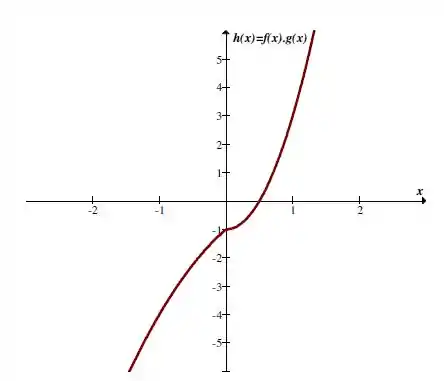
Aqui é contínua em , pois então existe , existe e .
Passo 2
Aqui temos os gráficos das funções:
Para :
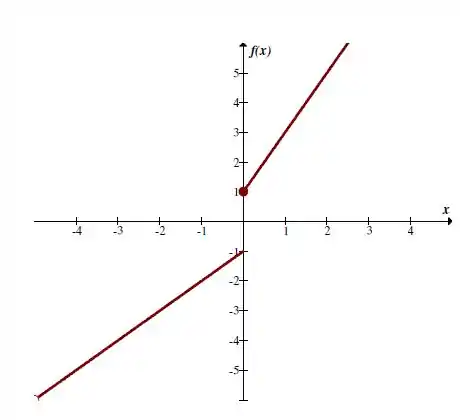
Agora para :
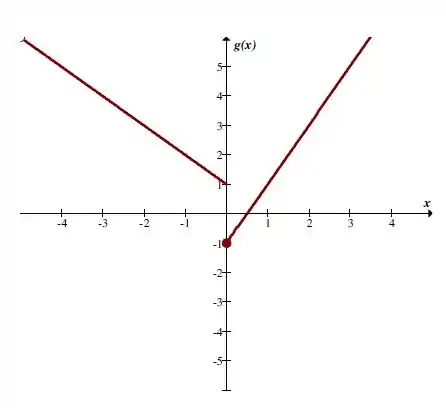
E para :