Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.6 - Ex. 9
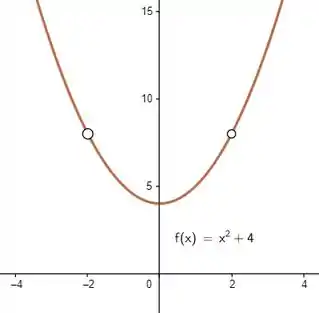
Nos exercícios de a , faça um esboço do gráfico da função; então, observando onde há quebras no gráfico, determine os valores da variável independente nos quais a função é descontínua e mostre por que a Definição não é satisfeita em cada descontinuidade
Passo 1
A primeira coisa que vamos notar aqui é que essa função pode ser reescrita se usarmos produtos notáveis. Afinal, temos diferença de quadrados em cima e em baixo. Se:
Então podemos escrever:
E ai a função fica:
Passo 2
Agora nota o seguinte. Pra função ser contínua pra qualquer escolhido deve ser satisfeito:
Como zeram o denominador de , esses são bons pontos pra gente testar:
Mas apesar do limite existir, nem nem estão definidos. Essa função então não vai ser contínua em e
Passo 3
Pra esboçar a gente pode cortar em cima e em baixo o que está em comum:
Basta esboçarmos a parábola e não marcarmos o ponto e já que eles não estão definidos:
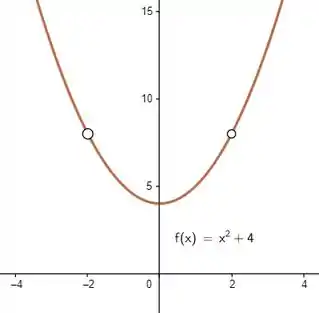
Resposta
Não definido em e
