Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.6 - Ex. 3
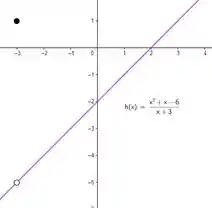
Nos exercícios de a , faça um esboço do gráfico da função; então, observando onde há quebras no gráfico, determine os valores da variável independente nos quais a função é descontínua e mostre por que a Definição não é satisfeita em cada descontinuidade
Passo 1
A primeira coisa que vamos notar aqui é no numerador da divisão de polinômios dentro dessa função definida por partes. Por ser de segundo grau, vale Bháskara. Bora fazer então:
Como temos ...
Show de bola, reescrevemos então a função para:
Passo 2
Pra gente ver onde a função é descontínua, temos que procurar pontos que “dão ruim”. Olha só, na divisão de polinômios, tem um único ponto que se encaixa:
Esse ponto é o já que ele zera o denominador. Note que apesar do limite...
...existir, e estar definido, não é uma verdade que:
Logo a função é descontínua em
Passo 3
Pra esboçar a gente pode cortar em cima e em baixo o que está em comum:
Basta esboçarmos a reta , não marcarmos o ponto , mas marcamos o ponto , já que este está definido:
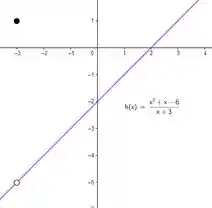
Resposta
Apesar de definido em , não é uma função contínua
