Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.Exercícios Práticos - Ex. 24
Nos Exercícios 23 e 24, use o gráfico para responder às questões.
24. Estime os intervalos onde a função é
a. crescente.
b. decrescente.
c. Use o gráfico de apresentado para indicar onde ocorrem os valores extremos locais da função e se cada extremo é um máximo ou um mínimo relativo.
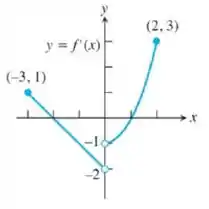
Passo 1
Nós temos o gráfico da derivada da função. Quando temos valores positivos para a derivada, seu coeficiente angular é positivo, ou seja ela está crescendo. E quando sua derivada é negativa ela está decrescendo. Logo,
a.
De e a função é positiva, ou seja, está crescendo.
b.
De e a função é negativa, ou seja, está decrescendo.
Passo 2
c.
Vamo analisar os dois pedaços separadamente.
No primeiro temos uma função crescente de até , onde atinge seu valor máximo, se torna decrescente e começa a diminuir até chegar em . Porém, a função não está definida para , ou seja, o mínimo local está em .
Na segunda parte podemos pensar da mesma forma, ela decresce até , onde atinge seu mínimo. A partir desse ponto aumenta até chegar em , como a função não está definida para podemos afirmar que o máximo local vai ser em
Resposta
a. e
b. e
c. Máximos locais: e . Minimos locais: e