Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.2 - Ex. 34
O gráfico de g consiste em duas retas e um semicírculo. Use-o para calcular cada integral.
Passo 1
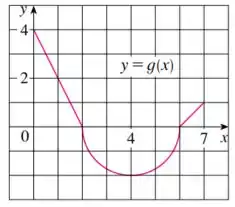
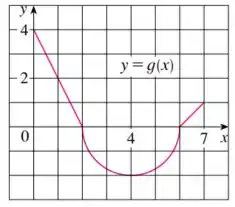
Eaee, belezinha?? Bom... o enunciado nos dá o seguinte gráfico de uma função :
E, através dele, devemos calcular as seguintes integrais:
Para isso, devemos entender que a integral é a área sob a curva e que uma integral de uma função é dada por:
Onde é o intervalo de integração!!
Agora bora lá!! 😉
Passo 2
Agora que sabemos disso já ficou mais fácil. Na letra a, vamos integrar a função de indo de até .
Se olharem no gráfico a figura formada abaixo da curva é um triângulo. Qual a área de um triângulo?
Sendo assim,
Passo 3
Na letra , a área formada acima da curva com indo de até é um semicírculo. Se a área do círculo é , então o semicírculo é .
Como estamos falando da área acima da curva:
Como o R é metade do diâmetro:
Substituindo:
Sendo assim:
Passo 4
Na letra c, vamos integrar a função de x indo de 0 até 7.
Já sabemos as áreas do intervalo de 0 até 6, então só precisamos achar a área de x indo de 6 até 7.
Se olharem no gráfico a figura formada abaixo da curva é um triângulo. E já sabemos a área:
Sendo assim,
Resposta
a)
b)
c)