Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 8.Parábola - Ex. 52
Na figura 8.21, o arco é parabólico e o segmento está dividido em 8 partes iguais. Sabendo que e , determinar .
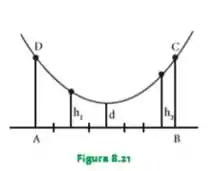
Passo 1
E aí, tudo joia?
Aqui vamos fazer o seguinte pra começar: vamos considerar que a origem do sistema de coordenadas é o ponto .
Daí, como o segmento , temos que:
Passo 2
Você pode ver também que, nesse caso, a reta diretriz da parábola é . E como , o vértice é (são 8 partes iguais, então cada pedacinho vale ).
Ok, já temos o vértice e a diretriz. O foco fica unidades acima do vértice, então:
Beleza, daqui a gente consegue escrever a equação da parábola!
Passo 3
Montando a equação:
Belezaaa! Essa é a equação da parábola!
Pra descobrir onde interceptam a parábola, é só a gente fazer o valor dela nos pontos do eixo .
Passo 4
Veja que está na abcissa e está na abcissa .
Vamos ver o ponto que essas abcissas representam na parábola:
Temos o ponto pertencendo à parábola então.
Vamos ver em , onde :
Temos um outro ponto da parábola então que é:
Passo 5
E agora, por fim, vamos calcular a medida de e . Já temos os pontos das extremidades, então para calcular o comprimento é só calcular a distância entre os pontos das extremidades de cada um...
Em :
E :
Que na realidade são os mesmos valores das alturas (valores de ) que a gente achou, então basicamente a gente precisava ver o valor dos pontos na parábola!
E acabamos😊