Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 5.10 - Ex. 35
Nos exercícios 35 a 43, determinar os valores máximo e mínimo da função dada, na região indicada.
35. ; no retângulo de vértices e .
Passo 1
Então pessoal, fazendo um esboço do retângulo, teremos o seguinte:
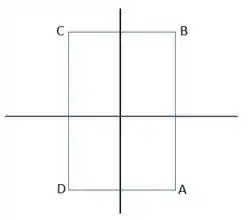
Nessa questão em específico não temos pontos críticos no interior do retângulo, uma vez que:
Então isso facilita bastante o nosso problema, pois só devemos fazer análise das fronteiras, ok?! Então bora lá!
Passo 2
Para facilitar a visualização vamos analisar cada segmento de reta separadamente, tudo bem? A função que nos foi dada é a seguinte:
Para o segmento temos que , então:
Então podemos concluir que nesse segmento não há pontos críticos! Ademais, testando os intervalos de , teremos:
Para o segmento temos que , então:
Então podemos concluir que nesse segmento não há pontos críticos! Ademais, testando os intervalos de , teremos:
Tudo bem, metade da análise já foi feita, então vamos para as duas finais!
Passo 3
Para o segmento temos que , então:
Então podemos concluir que nesse segmento não há pontos críticos! Ademais, testando os intervalos de , teremos:
Por fim, para o segmento temos que , então:
Então podemos concluir que nesse segmento não há pontos críticos! Ademais, testando os intervalos de , teremos:
Tudo bem, terminamos a análise das fronteiras! Se analisarmos todos os pontos que substituímos, fica tranquilo conconcluirmos o seguinte, se liga:
O ponto é ponto de mínimo e tem valor de e o ponto é ponto de máximo e tem valor de .
E está aí nossa análise dos máximos e mínimos da função que nos foi dada!
Resposta
Ponto de mínimo: , valor: ;
Ponto de máximo: , valor: .