Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 5.10 - Ex. 43
Nos exercícios 35 a 43, determinar os valores máximo e mínimo da função dada, na região indicada.
43. ; e .
Passo 1
Então galera, antes de começarmos a análise dos máximos e mínimos vamos esboçar o gráfico do domínio que queremos analisar:
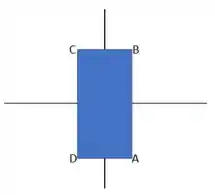
Antes de analisarmos as fronteiras vamos analisar o interior da figura para ver se há algum ponto crítico, beleza? Para fazermos isso temos que encontrar as derivadas parciais da nossa função e depois igualar os resultados a zero, saca só:
Igualando a zero:
Da primeira equação temos que:
Substituindo na segunda equação, teremos:
Sendo assim, temos que os pontos críticos no interior do retângulo são: e .
Passo 2
Agora que encontramos os pontos críticos do interior do retângulo, temos que analisar as fronteiras! Para o segmento temos que . Dessa forma:
Derivando e igualando a zero:
Sendo assim, do resultado podemos tirar que outros pontos críticos são e . Para o segmento temos que . Dessa forma:
Derivando e igualando a zero:
Sendo assim, do resultado não podemos tirar nada, uma vez que nosso conjunto está estabelecido nos reais.
Passo 3
Para o segmento temos que . Dessa forma:
Derivando e igualando a zero:
Assim como no passo anterior, desse resultado não podemos tirar nada, uma vez que nosso conjunto não está definido nos complexos. Por fim, para o segmento temos que . Dessa forma:
Derivando e igualando a zero:
Sendo assim, do resultado obtido podemos tirar que outros pontos críticos são: e . No entanto, esses pontos não fazem parte da restrição estabelecida pelo enunciado! Resumindo, temos o seguinte:
O ponto é ponto de mínimo e tem valor de e o ponto é ponto de máximo e tem valor de .
E está aí nossa análise completa dos máximos e mínimos da função em questão, pessoal! 😊
Resposta
Ponto de mínimo: , valor: ;
Ponto de máximoo: , valor: .