Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 11.2 - Ex. 42

Nos Exercícios 41 e 42, faça um esboço do gráfico de f , determinando primeiro os extremos relativos de f e as assíntotas horizontais do gráfico, se existirem.

42 .             f x = x x ,         x > 0  

Passo 1

Primeiro vamos determinar os extremos relativos de f . Para isso, devemos derivar e igualar a derivada a 0 .

Para derivar, vamos escrever f ( x ) da seguinte forma:

f x = x x = e ln ⁡ x x = e x ⋅ ln ⁡ x

Utilizando a regra do produto, a derivada vai ser:

f ' x = e x ln ⁡ x ⋅ x ln ⁡ x ' = e ln ⁡ x x ln ⁡ x + x x = x x ( ln ⁡ x + 1 )

f ' x = x x ( ln ⁡ x + 1 )

f ' x = 0 quando ln ⁡ x + 1 = 0       →       ln ⁡ x = - 1       →         x = e - 1 . Para x > e - 1 , f ' x > 0 e para 0 < x < e - 1 , f ' x < 0 . Isso nos indica que, quando x = e - 1 , nós temos um ponto de mínimo relativo.

f e - 1 = 1 e 1 e ≈ 0,69

É o mínimo relativo de f .

Ainda da análise acima, podemos perceber que a função é decrescente no intervalo ( 0 , e - 1 ) e crescente no intervalo ( e - 1 , + ∞ ) .

Passo 2

Agora vamos ver o que acontece quando l i m x → 0 + f ( x ) e l i m x → + ∞ f ( x ) .

Primeiro vamos ver quando x → 0 + .

l i m x → 0 + x x = l i m x → 0 + e x ⋅ ln ⁡ x = l i m x → 0 + e ln ⁡ x 1 x = e l i m x → 0 + ln ⁡ x 1 x = e ∞ ∞

Como tivemos a indeterminação ∞ ∞ , vamos usar a regra de Lhôpital.

l i m x → 0 + ln ⁡ x 1 x = l i m x → 0 + 1 x - 1 x 2 = l i m x → 0 + 1 - 1 x = l i m x → 0 + - x = 0

Sendo assim,

l i m x → 0 + x x = e l i m x → 0 + ln ⁡ x 1 x = e 0 = 1

l i m x → 0 + x x = 1

Agora vamos ver se existe alguma assíntota horizontal, fazendo l i m x → + ∞ f ( x ) .

l i m x → + ∞ x x = l i m x → + ∞ e x ⋅ ln ⁡ x = e l i m x → + ∞ x ⋅ ln ⁡ x = e + ∞ ⋅ + ∞ = + ∞

Como l i m x → + ∞ x x = + ∞ , não temos assíntotas horizontais.

Passo 3

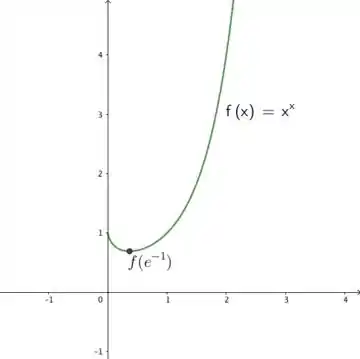
Agora vamos unir as informações em um gráfico.

1) f e - 1 ≈ 0,69 é o mínimo relativo, que também é o mínimo absoluto.

2) A função é decrescente no intervalo ( 0 , e - 1 ) e crescente no intervalo ( e - 1 , + ∞ ) .

3)   l i m x → 0 + f = 1 .

3)   l i m x → + ∞ f = + ∞ .

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o limite. Use a Regra de L'Hôspital quando for apropriado. Se existir um método mais elementar, use-o. Se a Regra de L'Hôspital não for aplicável, explique por quê. lim x → 1 ⁡ x 9 - 1 x 5 -
Encontre o limite. Use a Regra de L'Hôspital quando for apropriado. Se existir um método mais elementar, use-o. Se a Regra de L'Hôspital não for aplicável, explique por quê. lim x → 1 ⁡ ln ⁡ x sen ⁡ π
Encontre o limite. Use a Regra de L'Hôspital quando for apropriado. Se existir um método mais elementar, use-o. Se a Regra de L'Hôspital não for aplicável, explique por quê. lim x → 1 ⁡ x a - 1 x b -
Encontre o limite. Use a Regra de L'Hôspital quando for apropriado. Se existir um método mais elementar, use-o. Se a Regra de L'Hôspital não for aplicável, explique por quê. lim x → π 2 + ⁡ cos ⁡ x 1
Encontre o limite. Use a Regra de L'Hôspital quando for apropriado. Se existir um método mais elementar, use-o. Se a Regra de L'Hôspital não for aplicável, explique por quê. lim x → ∞ ⁡ ln ⁡ x x