Nos exercícios de 57 a 62, faça um esboço do gráfico da função; então, observando as quebras no gráfico, determine os valores da variável independente nos quais a função é descontínua e mostre, em cada caso de descontinuidade, por que a Definição 2,6,1 não é satisfeita.
59)
Passo 1
Precisamos avaliar os limites laterais dos valores limítrofes das condições () para entender como a função se comporta na região desses valores.
Passo 2
O gráfico da funçãoserá:
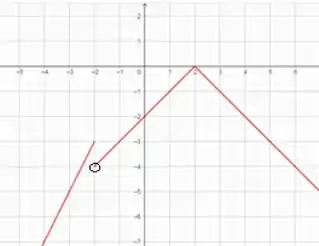
Passo 3
Agora vamos verificar as condições da Definição 2.6.1
Portanto, a função é continua em e descontínua em
Resposta
Gráfico da função:
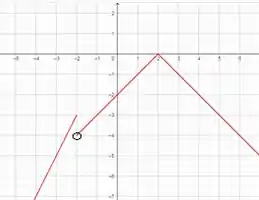
A função é descontínua em