Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.5 - Ex. 65e

Nos Exercícios 65 e 66, use um SAC para efetuar as integrações.

65 - Calcule as integrais

  1. ∫ x ln ⁡ x   d x
  2. ∫ x 2 ln ⁡ x   d x
  3. ∫ x 3 ln ⁡ x   d x
  4. Que padrão você observa? Determine a fórmula para ∫ x 4 ln ⁡ x   d x e depois confira se ela está correta calculando-a com um SAC.
  5. Qual é a fórmula para ∫ x n ln ⁡ x   d x ,   n ≥ 1 ? Confira a resposta com um SAC.

Passo 1

Resolveremos o item E, primeiramente de forma manual e depois conferir com o Maple:

Utilizaremos o método de substituição por partes:

∫ u   d v = u v -   ∫ v   d u

Consideraremos assim:

u = ln ⁡ x d v = x n d x

d u = u ' d x = 1 x d x

v =   ∫ x n   d x = x n + 1 n + 1

Substituindo:

∫ x n ⋅ ln ⁡ x d x = x n + 1 n + 1 ⋅ ln ⁡ x - ∫ x n + 1 n + 1 ⋅ 1 x d x

∫ x n ⋅ ln ⁡ x d x = x n + 1 n + 1 ⋅ ln ⁡ x - 1 n + 1 ∫ x n + 1 x d x

Utilizaremos uma regrinha de Matemática Básica pararesolver o expoente, que é a divisão de potência de mesma base, assim:

x n + 1 x 1 = x n + 1 - 1 = x n

∫ x n ⋅ ln ⁡ x d x = x n + 1 n + 1 ⋅ ln ⁡ x - 1 n + 1 ∫ x n d x

∫ x n ⋅ ln ⁡ x d x = x n + 1 n + 1 ⋅ ln ⁡ x - 1 n + 1 ⋅ x n + 1 n + 1

Logo:

∫ x n ⋅ ln ⁡ x d x = x n + 1 n + 1 ⋅ ln ⁡ x - x n + 1 n + 1 2

Passo 2

Resolveremos o item E, utilizando o software Maple.

- Criaremos um novo arquivo em modo folha de trabalho, seguindo os passos:

Arquivo > Novo > Modo Folha de Trabalho

Pronto agora utilizaremos o software para realizar o exercício solicitado.

Utilizaremos o seguinte comando:

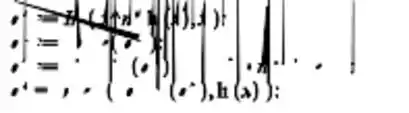
O termo

Onde q5 é o nome da equação, ≔ é o sinal de recebe um valor, a expressão:

Int(x^n*ln(x),x); Significa que queremos integrar x n l n x em d x .

Para que seja exibido o resultado no software basta pressionar enter.

O software retornará da seguinte forma:

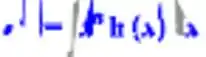
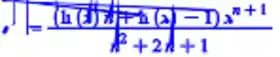
Assim fica resolvido este item utilizado o software.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule as integrais dos Exercícios 1-4635- ∫ 0 3 2 + 1 x 2 d x
59- Demonstre que, para qualquer número a1 , ∫ 1 a ln ⁡ xd x + ∫ 0 ln ⁡ a e y d y = a ln ⁡ a Veja a figura a seguir
Linearização de l n ⁡ ( 1 + x ) em x = 0 Em vez de aproximar ln x em x = 1, aproximamos ln ( 1 + x) em x =0. Dessa maneira, obten1os uma fórmula mais simples.Deduza a linearização ln ⁡ 1 + x ≈ x em x
58 – Linearização de e x em x = 0 Derive a aproximação linear e x ≈ 1 + x em x = 0 .Calcule a magnitude do erro envolvido na substituição de e x por 1 + x no intervalo [ 0 ; 0,2 ] . A resposta deve te
60- Desigualdade satisfeita pelas médias geométricaDemonstre que o gráfico de e x é côncavo para cima em qualquer intervalo de valores de x .Demonstre, em relação à figura a seguir, que, se 0ab , entã