Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.3 - Ex. 10
Nos exercícios 7-14, utilize os gráficos para determinar e que para todo
Passo 1
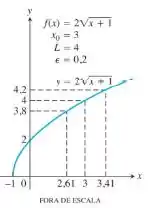
O que precisamos fazer nesses exercícios é dizer qual a distância do ponto que podemos ir sem que a imagem fique muito longe do valor .
Na grande maioria das vezes esse valor vai ser a distância entre e o valor de onde a função vale
Passo 2
O valor de é:
O valor de que tem imagem é
Logo, o nosso delta vale:
Isso está de acordo com o gráfico pois todos os valores de entre e estão com a imagem entre e !
Resposta
Exercícios de Livros Relacionados
Nos exercícios de 21 a 39, encontre o limite e, quando aplicável, indique os teoremas de limite usados. 34 )lim x → 1 x 3 - 1 x - 1
Nos exercícios de2 1 a 39, encontre o limite e, quando aplicável, indique os teoremas de limite usados. 2 8 )lim s → 1 s ³ - 1 s - 1 ³
Nos exercícios de 2 1 a 39, encontre o limite e, quando aplicável, indique os teoremas de limite usados. 30 )lim t → 3 2 8 t ³ - 27 4 t ² - 9 ³ ²
Nos exercícios de 21 a 39, encontre o limite e, quando aplicável, indique os teoremas de limite usados. 33 )lim x → 0 x + 2 - 2 x
Se f x = x ² + 5 x - 3 , ² mostre que lim x → 2 f x = f ( 2 ) .