Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.5 - Ex. 42

O gráfico da função abaixo possui alguma tangente horizontal no intervalo 0 ≤ x ≤ 2 π ? Se sim, onde? Se não, por quê? Visualiza os resultados representando as funções com uma ferramenta gráfica

y = x + 2 c o s x

Passo 1

Antes de começarmos a discutir sobre a questão, precisamos relembrar o que significa uma tangente horizontal. Uma tangente horizontal nada mais é do que uma reta paralela ao eixo X. Em outras palavras, uma reta horizonta, uma reta cuja a inclinação é nula, a derivada de uma função é igual 0.

Desta forma, nesta questão, precisamos verificar se há uma tangente horizontal tanto matematicamente quanto graficamente. Matematicamente isto será verificado a partir da derivada nula. Já graficamente, isto será verificado através de pontos de máximo e mínimos locais e/ou globais (reta tangente neste ponto).

Passo 2

Vamos começar a nossa questão pela análise matemática. Para isto, precisamos derivar a função y . Sendo assim, temos:

y ' = x + 2 c o s x '

y ' = 1 - 2 s e n ( x )

Passo 3

Como queremos encontrar uma reta horizontal, temos que fazer y ' = 0 . Portanto, temos:

y ' = 1 - 2 s e n ( x ) = 0

s e n ( x ) = 1 2

Dentro do intervalo 0 ≤ x ≤ 2 π , o valor de s e n ( x ) será igual a 1 / 2 quando x = π / 6 e quando x = 5 π / 6 .

Passo 4

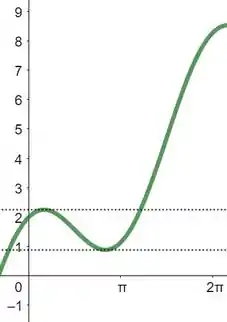
Vejamos abaixo no gráfico da função que há um ponto de máximo e de mínimo global em x = π / 6 e em x = 5 π / 6 respectivamente. Além disto, pode-se visualizar as retas tangentes horizontais.

Resposta

Existe tangentes horizontais nos pontos x = π / 6 e x = 5 π / 6

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para cada aproximação inicial, determine graficamente o que acontecerá se for usado o método de Newton para a função cujo gráfico é dado.(b) x 1 = 1
Para cada aproximação inicial, determine graficamente o que acontecerá se for usado o método de Newton para a função cujo gráfico é dado. ( b) x 1 = 1
Suponha que a reta tangente à curva y = f x no ponto ( 2,5 ) tenha a equaçãoy = 9 - 2 x . Se for usado o método de Newton para localizar uma raiz da equação f x = 0 com a aproximação inicial x 1 = 2 ,
Siga as instruções do Exercício 1(a), mas use x 1 = 9 como a aproximação inicial para encontrar a raiz s .
Para cada aproximação inicial, determine graficamente o que acontecerá se for usado o método de Newton para a função cujo gráfico é dado.(e) x 1 = 5