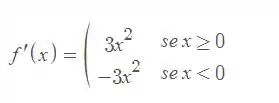Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.7 - Ex. 53
Nos Exercícios de 51 a 54, ache a derivada da função dada. (Sugestão: |a| = )
Passo 1
Para resolvermos este tipo de questão é fundamental que lembramos o conceito de função modular , bem como saibamos aplicar as regras de derivação ensinadas ao longo do capítulo. Sabemos que do conceito de função modular , temos
Passo 2
A partir do conceito de função modular, podemos escrever a função f(x) dada no enunciado como
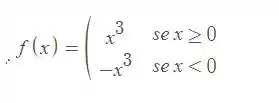
Passo 3
Com isso, temos que a derivada da função em questão será a seguinte
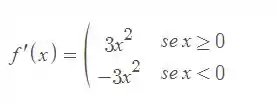
Resposta
Exercícios de Livros Relacionados
Derive as funções e determine o coeficiente angular da tangente no valor dado da variável independente. y=x+3 1-x ,x= - 2
Use a fórmula d y d x=lim z → x f ( z )-f ( x ) z-x Para determinar a derivada da função g ( x )=1+x
Use a fórmula d y d x=lim z → x f ( z )-f ( x ) z-x Para determinar a derivada da função f ( x )=x 2-3 x+4
Derive as funções e determine o coeficiente angular da tangente no valor dado da variável independente. s ( τ )=τ3 -τ 2 , τ=- 1
Derive as funções. Depois, determine uma equação para a tangente no ponto indicado no gráfico da função. w=g ( z )=1+4-z ,( z , w )=( 3,2 )