Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 6.6 - Ex. 3
Nos exercícios de 2 a 6, calcular, usando a definição, a derivada direcional no ponto e direção indicados.
,
Passo 1
Bom galera, este parece ser mais difícil, mas não !
Segundo o problema, o ponto Q só irá alterar somente no eixo positivo de z.
Então, o ponto Q terá as coordenadas .
Desenhando:
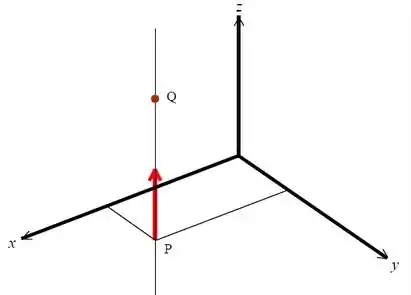
Passo 2
Agora nós vamos aplicar a definição 6.3.1:
Substituindo nossas coordenadas:
Sabendo que a função é :
E:
Agora nós substituímos:
Resolvendo o limite:
Finalizamos galeraa!
Resposta
Exercícios de Livros Relacionados
Quais das seguintes afirmações são verdadeiras se ƒ(x, y) é diferenciável em (x0, y0)? Justifique suas respostas.a. Se u é um vetor unitário, a derivada de ƒ em (x0, y0) na direção de u é (ƒx(x0, y0)i
Derivada direcional máxima Qual é o maior valor que a derivada direcional de ƒ(x, y, z) = xyz pode ter no ponto (1, 1, 1)?
Nos Exercícios 37-40, encontre as direções nas quais ƒ cresce e decresce mais rapidamente em P0 e encontre a derivada de ƒ em cada direção. Encontre também a derivada de ƒ em P0 na direção do vetor v.
Derivadas direcionais com valores dados No ponto (1, 2), a função ƒ(x, y) tem uma derivada de 2 na direção (2, 2) e uma derivada de –2 na direção (1, 1).a. Encontre ƒx (1, 2) e ƒy (1, 2).b. Encontre a
Nos Exercícios 37-40, encontre as direções nas quais ƒ cresce e decresce mais rapidamente em P0 e encontre a derivada de ƒ em cada direção. Encontre também a derivada de ƒ em P0 na direção do vetor v.