Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 6.6 - Ex. 2
Nos exercícios de 2 a 6, calcular, usando a definição, a derivada direcional no ponto e direção indicados.
, .
Passo 1
Bora começar?!
Então galera, a primeira coisa a fazer aqui é achar o vetor unitário de que nós vamos chamar de .
Se lembram como calcular o vetor unitário??
Bem fácil, não é?!
Pelo problema nós sabemos que:
E é dado por:
Substituindo:
Passo 2
Agora nós vamos desenhar um triângulo retângulo em que :
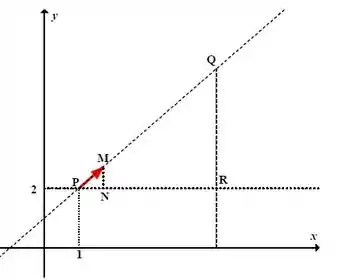
Como o triângulo é semelhante ao :
Então, as coordenadas do ponto Q será o ponto P mais as medidas que acabamos de achar, não é?
Sendo assim, as coordenadas de Q serão
Passo 3
Agora nós vamos aplicar a definição 6.3.1:
Substituindo nossas coordenadas:
Sabendo que a função é :
E:
Agora nós substituímos:
Resolvendo o limite:
Racionalizando:
Finalizamos galeraa!
Resposta
Exercícios de Livros Relacionados
Mostre que a função f x , y = x y 3 é contínua e suas derivadas parciais f x e f y existem na origem, mas as derivadas direcionais em todas as outras direções não existem.Traçe o gráfico de f perto da
Nos Exercícios 11-18, encontre as derivadas da função em P 0 na direção de u . f x ,y ,z = x y + y z + z x , P 0 1 ,- 1 ,2 ,u = 3 i + 6 j - 2 k
Nos Exercícios 11-18, encontre as derivadas da função em P 0 na direção de u . f x ,y ,z = x 2 + 2 y 2 - 3 z 2 , P 0 1 ,1 ,1 ,u = i + j + k
Nos Exercícios 11-18, encontre as derivadas da função em P 0 na direção de u . f x ,y ,z = 3 e x cos y z , P 0 0 ,0 ,0 ,u = 2 i + j - 2 k
Nos Exercícios 11-18, encontre as derivadas da função em P o na direção de u . h x , y , z = cos x y + e y z + ln z x P 0 = 1 ,0 ,1 / 2 u = i + 2 j + 2 k