Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 7.4 - Ex. 28

Nos exercícios de 15 a 36, calcule a integral indefinida. (28) ∫ 5 - 4 y ² 3 + 2 y d y

Passo 1

Nessa questão aqui vamos usar uma coisa que aprendemos no ensino médio e que nunca achamos que fossemos aplicar. Esse momento chegou! Temos na nossa integral uma divisão de polinômios que precisa ser efetuada para conseguirmos resolvê-la.

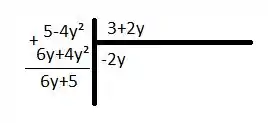
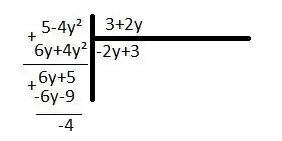
Podemos escrever, então, da seguinte forma:

5 - 4 y 2 = 3 + 2 y 3 - 2 y - 4

Vamos dividir os dois lados da expressão por 3 + 2 y .

5 - 4 y 2 3 + 2 y = 3 + 2 y 3 - 2 y 3 + 2 y - 4 3 + 2 y

Fazendo as possíveis simplificações na expressão, temos:

5 - 4 y 2 3 + 2 y = 3 - 2 y - 2 × 2 3 + 2 y

Depois da divisão polinomial, conseguimos encontrar uma forma simplificada da expressão inicial, possibilitando a resolução da nossa integral! Vamos substituir ela para ver como fica:

f y = ∫ 5 - 4 y 2 3 + 2 y d y = ∫ - 2 y + 3 - 2 × 2 3 + 2 y d y f x = ∫ - 2 y   d y + ∫ 3 d y - ∫ 2 × 2 3 + 2 y d y

A primeira e a segunda integral são tranquilíssimas de resolver né, galera? Vamos integrar pra ver o resultado:

∫ - 2 y   d y = - 2 y 2 2 + C = - y 2 + C ∫ 3 d y = 3 y + C

Passo 2

A segunda integral pode ser facilmente resolvida usando o método da subsituição. Vamos fazer u = 3 + 2 y → d u = 2 d y   e substituir na integral:

∫ 2 × 2 3 + 2 y d y = 2 ∫ d u u

Agora está mais fácil de resolver! Essa integral já é uma velha conhecida nossa.

2 ∫ d u u = 2 ln ⁡ u + C

Se começamos a questão com a variável x , vamos voltar para ela a fim de escrever parte da resposta.

2 ln ⁡ 3 + 2 y + C

Resposta

O resultado é:

∫ 5 - 4 y ² 3 + 2 y d y = - y 2 + 3 y - 2 ln ⁡ 3 + 2 y + C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a Integral abaixo:12 - int cos^3 2 x sen^5 2 x d x
Resolve a integral abaixo:28 – ∫ 0 π / 6 1 + s e nxd x Dica: Multiplique por 1-s e nx 1 - s e nx
Resolve a integral abaixo:27 – int_(pi // 3)^(pi // 2) (s e n^2 x)/(sqrt(1 - cos x)) d x
g)int_1^2 (3 s)/(1 + s^2) d s
f) int_0^1 x sqrt(1 + 2 x^2) d x