Nos exercícios de 1 a 6, coloque num gráfico o ponto P dado e cada um dos seguintes pontos: a) O ponto Q, tal que a reta que passa por P e Q seja perpendicular ao eixo x e o divida ao meio. Dê as coordenadas de Q.

b) O ponto R, tal que a reta que passa por P e R seja perpendicular ao eixo y e o divida ao meio. Dê as coordenadas de R.

c) O ponto S, tal que o segmento que passa por P e por S seja dividido ao meio pela origem. Dê as coordenadas de S. d) O ponto T, tal que o segmento de reta que passa por P e T seja perpendicular e dividido pela reta que passa pela origem, formando um ângulo de 45◦ e dividindo o primeiro e o terceiro quadrantes. Dê as coordenadas de T.

5) P (-1,-3)

1. Observe que o ponto Q pedido é o simétrico de P em relação ao eixo x, portanto Q (-1,3).



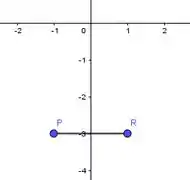
2. Observe que o ponto R pedido é o simétrico de P em relação ao eixo y, portanto R(1,-3).



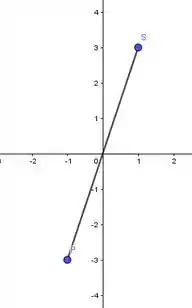
3. Observe que o ponto S pedido é o simétrico de P em relação à origem, portanto S(1,3).



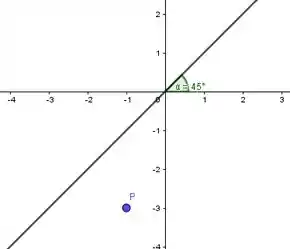
4. Observe que a reta que corta o primeiro e terceiro quadrantes formando 45◦ é a reta y = x

O ponto que queremos encontrar é o simétrico de P em relação a reta . Vamos determinar a equação da reta que passa por P e seja perpendicular à reta . Para isso precisamos que o coeficiente angular da reta seja , pois o produto das inclinações dessas retas será -1. Assim

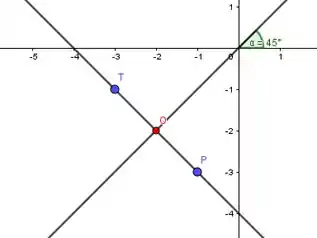
Assim temos o seguinte esboço

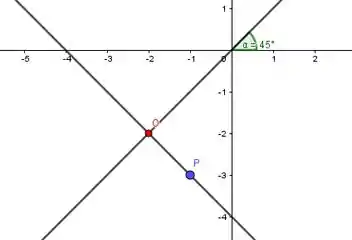
Vamos agora encontrar o ponto O que é a interseção entre essas duas retas. Assim

Logo o ponto O, por pertencer a reta , será .

Para finalizar, devemos encontra o ponto T de forma que o segmento PO tenha o mesmo tamanho do segmento OT, ou seja, O seja o ponto médio de PT. Assim, tomando T(x,y) genérico, temos

Montando o sistema temos

Portando, o ponto será T(-3,-1).