Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.6 - Ex. 5
Nos Exercícios 5 a 12, determine o valor exato da função.
5. a) ; b) ; c) ; d) ;
Passo 1
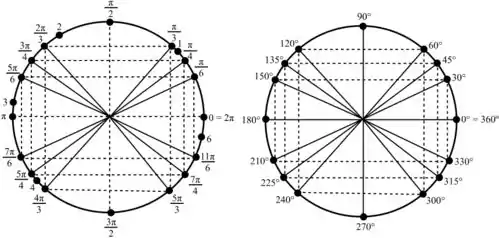
Vamos usar os círculos trigonométricos abaixo para resolver.
Passo 2
Passo 3
Passo 4
Passo 5
Resposta
Exercícios de Livros Relacionados
27. b. Faça um gráfico y = s en x e y = cos sec x juntos para - π ≤ x ≤ 2 π . Comente o comportamento de cos sec x em relação aos sinais e valores de s e n ( x )
Faça os gráficos das funções nos Exercícios 23-26 no plano t s (eixo t horizontal, eixo s vertical). Qual é o período de cada função? Que simetrias os gráficos possuem?25. s = s e c π t 2
Use as fórmulas para adição para deduzir as identidades nos Exercicios 31-36.31. cos x - π 2 = s e n x
Use as fórmulas para adição para deduzir as identidades nos Exercicios 31-36.35. cos A - B = cos A cos B + sen A sen B
Use as fórmulas para adição para deduzir as identidades nos Exercicios 31-36.36. sen A - B = sen A cos B - cos A sen B