Nos exercícios 1 a 7, a equação dada é uma representação implícita de uma superfície S.
- Identificar a superfície.
- Escrever algumas representações explícitas de partes de S, representando graficamente.
Passo 1
Então galera, desenhando nossa superfície:
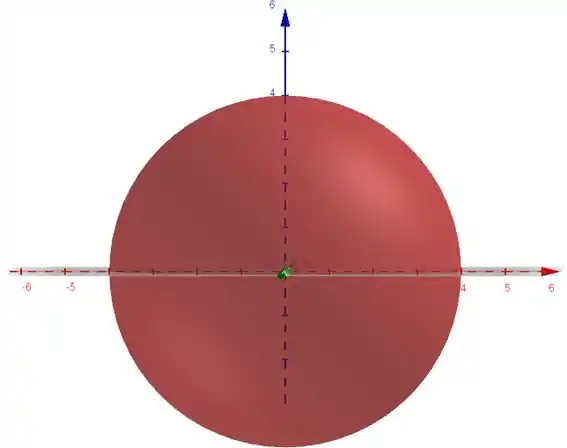
O que nos mostra uma figura de esfera, certo?
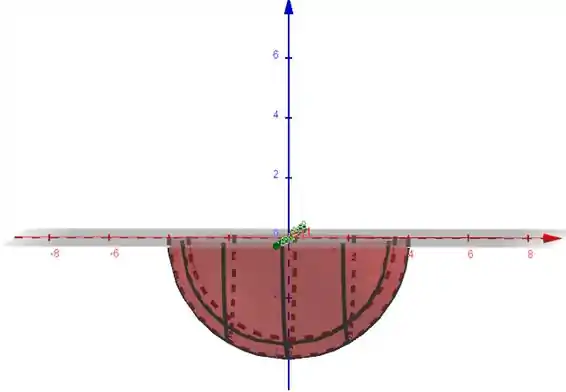
Para as equações explícitas nós isolamos uma das variáveis, começando por z:
Quando :
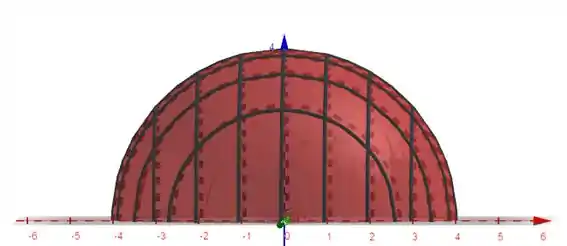
Quando :
Passo 2
Isolando y:
E x:
E os desenhos nós fazemos da mesma forma, ok?
E é isso aí, galera !!
E acabamos !!