Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 2.3 - Ex. 1
Nos exercícios a , esboce o gráfico da superfície de equação dada.
;;.
Passo 1
E aí, pessoal!! Bora pra mais um exercício com o Responde Aí? Vem com a gente :D
Pra começarmos esse exercício, precisamos lembrar do conceito de planos. Na seção do livro Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis - 1ª Ed., um plano tem a equação:
Onde é o vetor normal ao plano que passa pelo ponto .
Ainda, o Exemplo (página ) diz que um plano com equação passa pelo ponto e tem vetor normal . O único plano que possui essa normal é o plano coordenado .
Assim, podemos concluir que o plano de equação é paralelo ao plano .
Analogamente, se um plano possui equação ou , ele é paralelo ao plano ou passando pelo ponto ou , respectivamente.
Passo 2
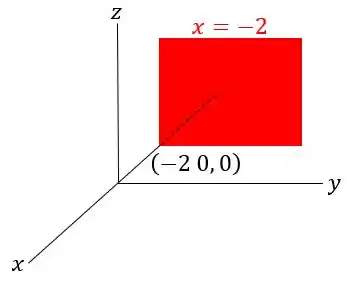
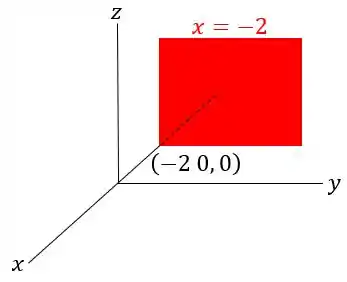
Então, para o nosso primeiro plano, a equação é:
Isso significa que ele passa pelo ponto , possui vetor normal e está localizado no plano .
Logo, esboçando isso:
Passo 3
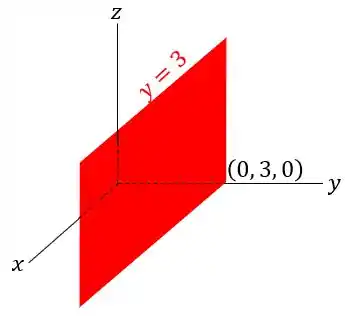
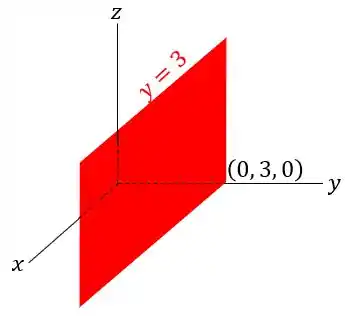
Analogamente, o segundo plano dado por:
Isso significa que ele passa pelo ponto , possui vetor normal e está localizado no plano .
O seu esboço, então, é:
Passo 4
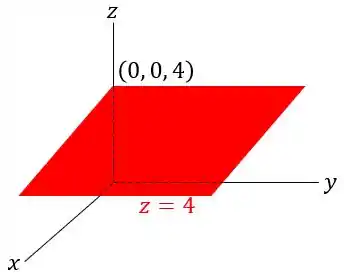
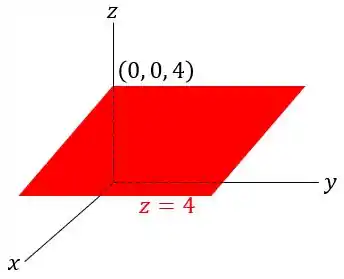
Por fim, mas não menos importante, o plano de equação:
Se localiza no plano , passando pelo ponto e com vetor normal . Isso pode ser mostrado esboçando-o a seguir:
Resposta
