Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 12.6 - Ex. 28
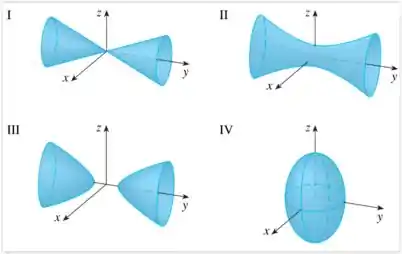
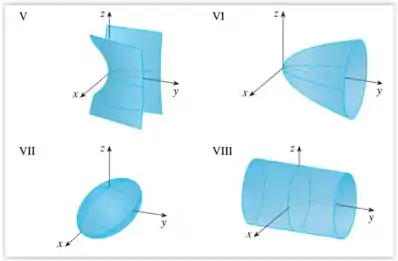
Faça uma correspondente entre a equação e seu gráfico (identificado por Justifique sua escolha.
Passo 1
A melhor maneira de identificar um sólido pela equação geral é realizar cortes sistemáticos em cada direção e visualizar que cônica estamos visualizando.
Passo 2
Vamos tomar nossa equação sugerido e fazer 3 cortes. Primeiro em , ficando com
Uma parábola no plano mas no sentido negativo.
Depois tomamos o corte no plano , ficando com
Uma parábola no plano no sentido positivo.
O último corte é feito no plano , no deixando com uma hipérbole. Desta forma podemos identificar nossa superfície como um Paraboloide hiperbólico.
A única figura com essas características é a
Resposta
Exercícios de Livros Relacionados
Use cortes para esboçar e identificar as superfícies. y = z 2 - x 2
Use cortes para esboçar e identificar as superfícies. x 2 = y 2 + 4 z 2
Use cortes para esboçar e identificar as superfícies. 25 x 2 + 4 y 2 + z 2 = 10 0
Faça uma correspondente entre a equação e seu gráfico (identificado por I - V I I I ). Justifique sua escolha. x 2 - y 2 + z 2 = 1
Faça uma correspondente entre a equação e seu gráfico (identificado por I - V I I I ). Justifique sua escolha. 9 x 2 + 4 y 2 + z 2 = 1