Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.2 - Ex. 20
Nos Exercícios 19-24, esboce a região de integração e calcule a integral.
Passo 1
Olá pessoal, primeiramente vamos esboçar a nossa região de integração, onde:
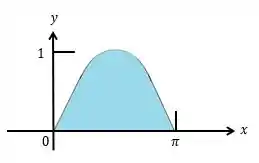
Do enunciado temos a seguinte integral:
Vamos, primeiro, derivar em função de :
Passo 2
Para resolvermos a integral, iremos colocar a constante para fora:
Além disso, sabemos que:
Logo:
Resposta
Exercícios de Livros Relacionados
As integrais e somas de integrais nos Exercícios 13-18 fornecem as áreas das regiões no plano xy. Esboce cada região, marque cada curva limitante com sua equação e forneça as coordenadas dos pontos on
Encontre o valor médio de ƒ (x , y) = (1)/(x y)ƒ sobre o quadrado l n 2 = x = 2 l n 2 , l n 2 = y = 2 l n 2 .
As integrais e somas de integrais nos Exercícios 13-18 fornecem as áreas das regiões no plano xy. Esboce cada região, marque cada curva limitante com sua equação e forneça as coordenadas dos pontos on
Nos Exercícios 1-12, esboce a região delimitada pelas retas e curvas dadas. Em seguida, expresse a área da região como uma integral dupla iterada e calcule a integral. ap a r a b o l ax = y - y 2ear e
As integrais e somas de integrais nos Exercícios 13-18 fornecem as áreas das regiões no plano xy. Esboce cada região, marque cada curva limitante com sua equação e forneça as coordenadas dos pontos on