Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.3 - Ex. 16

As integrais e somas de integrais nos Exercícios 13-18 fornecem as áreas das regiões no plano xy. Esboce cada região, marque cada curva limitante com sua equação e forneça as coordenadas dos pontos onde as curvas apresentam interseção. Em seguida, encontre a área da região.

∫ - 1 2 ∫ y 2 y + 2 d x   d y

Passo 1

Faaaala, cara! Tranquileba?

Nos exercícios anteriores tínhamos definido a integral pela função, agora de maneira contraria vamos encontrar a função pela integral. Sendo assim, nós temos que a função que limita os pontos é dado por x, veja que x = y 2 e vai até a função que a limita nesse intervalo, ou seja x = ( y + 2 ) . Se fizermos um esboço dessas funções temos:

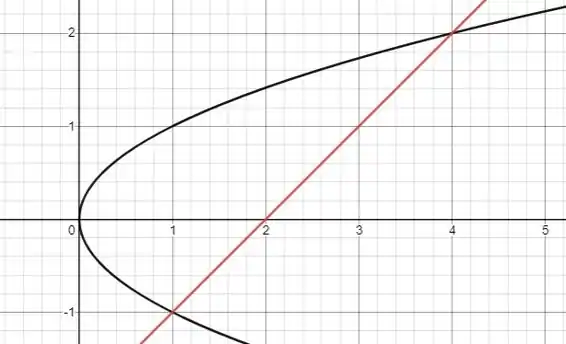
Onde temos, como mostrado na integral x indo de -1 a 2

Passo 2

Para acharmos os pontos de interseção, basta igualarmos as equações. Assim:

y 2 = y + 2

- y 2 + y + 2 = 0

y = - 1 ± 1 + 4 × 1 × 2 - 2

y 1 = 2

y 2 = - 1

Onde comprovamos pela figura que (-1,2) são de fato os pontos de interseção.

Passo 3

∫ - 1 2 ∫ y 2 y + 2 d x   d y

∫ - 1 2 y + 2 - y 2 d y

1 2 y 2 + 2 y - 1 3 y 3 - 1 2

2 + 4 - 2 3 3 - 1 2 - 2 + 1 3

9 2

Resposta

Os pontos de interseção são:

y 1 = 2

y 2 = - 1

Valor da integral:

9 2

Exercícios de Livros Relacionados

Determine o volume do sólido dado.Limitada pelos planos z = x , y = x , x + y = 2 e z = 0
Determine o volume do sólido dado.Limitada pelo cilindro y 2 + z 2 = 4 e pelos planos x = 2 y , x = 0 , z = 0 no primeiro octante
Determine o volume do sólido dado.Limitada pelos planos coordenados e pelo plano 3 x + 2 y + z = 6
Determine o volume do sólido dado.Delimitado pelo paraboloide z = x 2 + 3 y 2 e pelos planos x = 0 , y = 1 , y = x , z = 0
O mapa de contorno mostra a temperatura, em graus Fahrenheit, às 4 horas da tarde do dia 26 de fevereiro de 2007 , no estado do Colorado. (O estado mede 388 mi de leste a oeste e 276 mi de norte a sul