Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 8.2 - Ex. 10 b
Seja e Desenhe de sendo
b) e
Passo 1
Vamo desenhaar?Mas já? Assim e pá?Calmaa.. Como foi dado o valor de e , bora fazer a substituição no caminho e depois aplicar na função. Então, bora!
Substituindo os valores de e , o caminho fica
Perceba que
Daí,
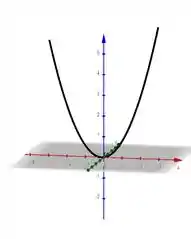
Então, agora vamos desenhar... Mas antes, se ligue numa parada: não temos nenhuma coordenada nula, então nossos caminho tá em . E mais, para cada valor de e dados, que são iguais, vamos ter ele ao quadrado, o que nos remete a uma parabola. E, comoo é positivo, tem concavidade para cima. Então, partiu!
Resposta
Exercícios de Livros Relacionados
Um ponto P descreve uma curva sobre o gráfico da função f ( x ,y )=x²+y² ² ² de modo que a sua projeção Q sobre o plano xy descreve a reta x+y=1 . Determine o ponto da curva que se encontra mais próxi
Raciocinando geometricamente, determine, caso existam, os valores máximo e mínimo de f em A , bem como os pontos em que estes valores são atingidos. f x , y = y x - 1 e A o círculo x - 3 2 + y - 1 2 ≤
Seja f x , y = x 2 x 2 + y 2 . Desenhe a imagem da curva γ t = ( x t , y t , z t ) , onde x t = Rc o s t ,y t = Rs e n t e z = f ( x , y ) (R0) . Como é o gráfico de f ?
Seja f x , y = x y e γ t = a t , b t , f a t , b t . Desenhe de γ sendo c) a = 1 e b = 0
Seja f x , y = x y e γ t = a t , b t , f a t , b t . Desenhe de γ sendo a = 0 e b = 1