Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 40
O índice de massa corporal é definido no exercício 39. Desenhe a curva de nível dessa função correspondente a alguém com 200 cm de altura e peso de 80 kg. Encontre os pesos e alturas de duas outras pessoas com mesma curva de nível.
Passo 1
Oie, meu amigo. Tudo bem? Vou te ajudar a resolver essa atividade!
Aqui a gente precisa dar uma olhada no exercício , pois precisamos da definição do IMC existente nele.
O índice de massa corporal é dado por
Então o que iremos fazer é desenhar uma curva de nível para essa função, onde e .
Para encontrar as curvas de nível dessa função, a igualamos a uma constante :
E escolhemos diversos valores reais para , e assim desenhamos o seu gráfico.
A equação acima descreve uma função quadrática passando pela origem.
Passo 2
Sabendo que a função é quadrática, que e temos:
Dessa maneira, a curva de nível que representa o IMC dessa pessoa é descrita pela parábola:
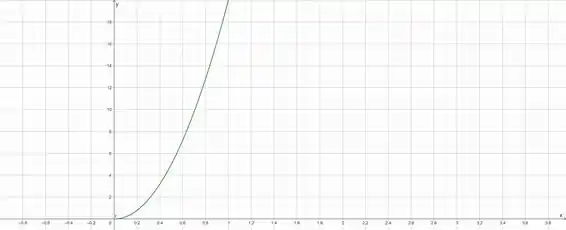
A curva é mostrada abaixo, onde o eixo representa a altura da pessoa, enquanto que o eixo representa a massa da mesma.
Passo 3
A partir do gráfico mostrado no passo , podemos concluir que uma pessoa que tem metro e 20 kg se encontra na mesma curva.
Podemos encontrar a segunda pessoa analiticamente, escolhendo por exemplo uma altura de m. Dessa, forma, inserindo m= na equação correspondente a essa curva de nível temos:
Ou seja, pessoa que tem massa de kg e altura de m também se encontra na mesma curva.
Resposta
A curva de nível correspondente à pessoa descrita no enunciado é
Duas pessoas que se encontram nessa mesma curva possuem massa e altura respectivamente iguais a