Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 45
Desenhe a curva de nível da função mostrando vários níveis.
Passo 1
E aí galerinha?
A função representada possui duas variáveis, o que significa que ela existe como superfície em um espaço tridimensional. Para cada valor de e existe um .
Para a melhor compreensão desse capítulo, no entanto estamos trabalhando o comportamento dessas funções no plano .
Para encontrarmos as curvas de nível de uma função de duas variáveis, fazemos
Desse modo conseguimos avaliar o recorte da função para o valor de constante. Ou seja, no plano , para cada k escolhido teremos um nível.
Nesta questão iremos encontrar como se comporta a função para esse valor fixo e em seguida esboçar um plano contendo as curvas de nível.
Passo 2
Igualando a função dada a uma constante , temos:
Se escolhermos , teremos um par de retas passando pela origem:
Para , vamos avaliar o comportamento pro caso específico em que :
Essa equação é de uma hipérbole cruzando o eixo .
Por último, caso tenhamos , como será que fica? Vamos fazer igual avaliando :
Ou seja, teremos uma hipérbole cruzando o eixo .
Passo 3
A forma de uma hipérbole no plano é conhecida. O problema nos dá dois tipos de hipérbole: Uma com concavidade direcionada ao eixo (caso ) e uma com convavidade direcionada ao eixo (caso ).
Por conta disso, queremos montar um gráfico para diferentes valores de , sendo cada um o representante de uma diferente curva de nível.
Ao esboçar as hipérboles no plano da forma descrita, temos o seguinte resultado
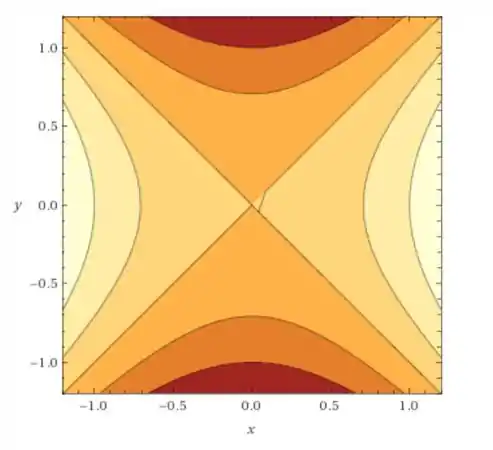
Resposta
As curvas de nível da função dada são um par de retas para , e hipérboles para diferente de 0, cujo eixo principal depende do sinal de .