Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 13
Encontre e esboce o domínio da função.
Passo 1
Falaaa aí! Tudo joinha?
Vamos matar mais essa? O que podemos fazer?
Esta questão pede para encontrarmos o domínio da função:
E como podemos fazer isso?
Primeiro vamos lembrar que o domínio de são os valores de e que podem ser usados para que seja real.
Para definir o domínio, é melhor olhar para as restrições.
Precisamos determinar as condições em que as expressões dentro das raízes quadradas são não-negativas, pois a raiz quadrada de um número negativo não é definida no conjunto dos números reais.
Vamos resolver?
Passo 2
Temos a soma de duas raízes, portanto, vamos olhar dentro de cada uma.
Na primeira:
Então,
Na segunda:
Então,
Passo 3
Logo, o domínio de é , esboçando o gráfico, temos:
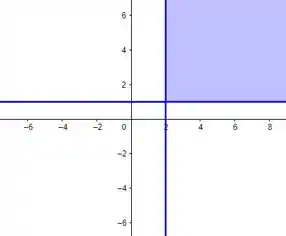
O gráfico do domínio da função mostra a região do plano onde e . Esta área é à direita da linha vertical e acima da linha horizontal . Ambas as linhas são incluídas no domínio, indicando que os pontos sobre essas linhas também são válidos. O domínio é, portanto, o quadrante superior direito a partir do ponto .
Resposta
é