Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 14
Encontre e esboce o domínio da função.
Passo 1
Temos a função
Note que, aqui, temos o radicando de uma raís de índice par (igual a ), então olhemos para o que tem dentro da raíz. Logo
Assim,
Passo 2
Logo, o domínio da função é
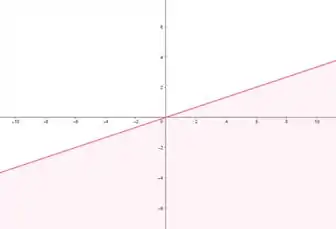
Para esboçar vamos ver a reta
Deixando o sozinho, como estamos acostumados, temos:
Depois de desenhar essa reta que a gente ta careca de saber, vamos rever a inequação
Entao é só pegar a reta e os valores abaixo dela, então nosso esboço fica:
Resposta
Exercícios de Livros Relacionados
Faça o mapa de contorno da função mostrando várias curvas de nível. f x , y = y 2 - x ² ²
Descreva as superfícies de nível da função. f x , y , z = x 2 - y 2 + z 2
Esboce um mapa de contorno e um gráfico da função e compare-os. f x , y = 36 - 9 x 2 - 4 y 2
Faça um esboço do diagrama de contorno da função cujo gráfico é mostrado.
(a) Mostre que, tomando logaritmos, a função geral de Cobb-Douglas P = b L α K 1 - α pode ser expressa como ln P K = ln b + α ln L K (b) Se tomarmos x = ln L K e y = ln P K , a equação da pa