Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 24
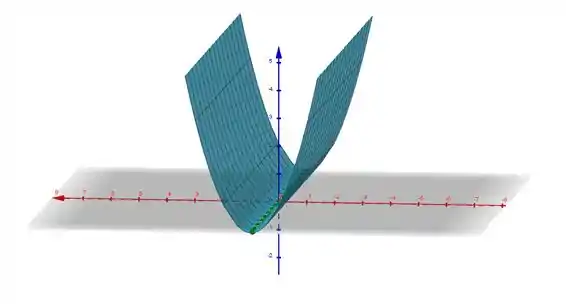
Esboce o gráfico da função.
Passo 1
E aí, pessoal. Beleza?
Aqui nessa questão nós temos a função e queremos esboçar o seu gráfico.
Para fazer isso, vamos primeiro entender um pouco mais sobre essa função e depois fazer o seu gráfico.
Tranquilo? Vem comigo então.
Passo 2
Temos que
Fazemos que
Se fossemos fazer esse gráfico apenas no plano , ele seria uma parábola que passa pelo primeiro e segundo quadrante.
Passo 3
Antes de fazer o gráfico, podemos olhar para a definição da função e ver que ela não depende de, ou seja, para qualquer valor de , nós sempre teremos uma parábola passando.
Logo, O gráfico corta o plano com uma parábola e pode assumir qualquer valor real.
Note que em funções de mais variáveis o gráfico não se encontra mais no plano 2D.
Assim, o gráfico fica na seguinte forma:
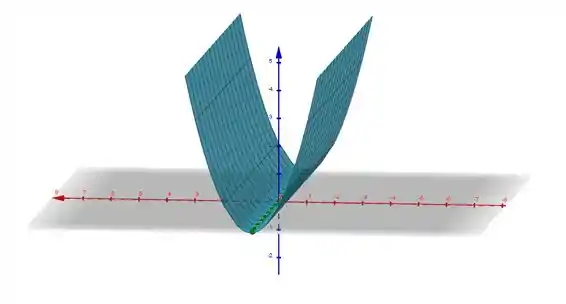
Resposta
