Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 10.3 - Ex. 41

Nos exercícios 21 a 45, escrever uma representação paramétrica para a superfície dada.

41 ) Parte do cone y = 1 - x 2 + z 2 ,   tal que y ≥ - 3 .

Passo 1

Então galera, desenhando nossa situação:

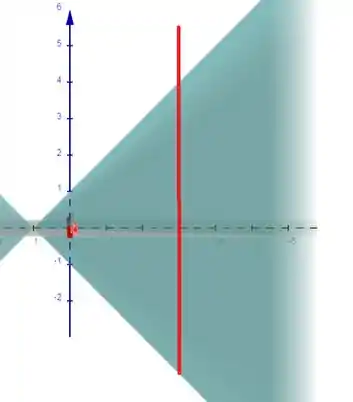
Neste caso nós temos um cone representado na forma explícita, então podemos parametrizá-lo fazendo:

x = u

z = v

y = 1 - u 2 + v 2  

Como, y ≥ - 3 :

1 - u 2 + v 2 ≥ - 3

- u 2 + v 2 ≥ - 4

u 2 + v 2 ≤ 4

u 2 + v 2 ≤ 16

Logo,

r → u , v = u i ^ + ( 1 - u 2 + v 2   ) j ^ + v k ^

E encontramos nossa equação parametrizada!!

Resposta

r → u , v = u i ^ + ( 1 - u 2 + v 2   ) j ^ + v k ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Faça uma correspondência entre as equações e os gráficos identificados por I - V I e justifique sua resposta. Determine quais famílias de curvas da grade têm u constante e quais têm v constante. x = s
Encontre as representações paramétricas das superfícies:A parte do cilindro x 2 + z 2 = 9 que está acima do plano x y e entre os planos y = - 4 e y = 4 .
Encontre as representações paramétricas das superfícies:A parte da esfera x 2 + y 2 + z 2 = 36 que está entre os planos z = 0 e z = 3 3 .
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A parte da superfície z = l
Encontre as equações paramétricas da superfície obtida pela rotação da curva x = 1 y , y ≥ 1 ao redor do eixo y e use-as para traçar o gráfico da superfície.