Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.2 - Ex. 23
Nos exercícios de 21 a 24, a região é limitada pelas curvas gira em torno do eixo indicado. Ache o volume do sólido gerado.
23.a reta
Passo 1
Vamos primeiro observar a figura abaixo para sabermos qual a região limitada pelas curvas:
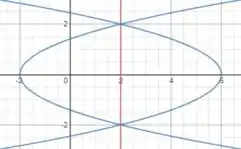
Primeiro escolhemos se o elemento retangular será vertical ou horizontal e então aplicamos a equação
Para obtermos o volume
Passo 2
Como dá para perceber pela imagem, ela é simétrica em relação à reta que estamos usando como eixo de rotação, por isso precisamos pegar apenas um dos lados para rotacionarmos, pegaremos o direito, que respeita a função.
Reescrevendo a função, para deixar x como variável:
Vamos considerar um elemento retangular vertical, então os limites de integração estarão escritos com relação a x, .
A equação então ficará da seguinte maneira:
O x da função anterior foi substituído por porque nós não estamos rotacionando em relação à origem.
Passo 3
Agora precisamos resolver a integral:
Fazendo a substituição , e os limites de integração passarão a ser , ficamos então com:
Invertendo os limites:
Integrando cada termo:
Substituindo os limites superior e inferior: