Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 10.Exercícios práticos - Ex. 76

Nos Exercícios 73-78:

a. Utilize séries de potências para avaliar o limite.

b. Em seguida, utilize um gráfico para provar seus cálculos

76. lim h → 0 ⁡ sen ⁡ h h - cos ⁡ h h 2

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Para esse caso, vamos manipular um pouco primeiramente esse limite, com isso, nós temos que

  lim h → 0 ⁡ sen ⁡ h h - cos ⁡ h h 2 =   lim h → 0 ⁡ 1 h ( h - h 3 3 ! + h 5 5 ! - … ) - 1 - h 2 2 ! + h 4 4 ! - … h 2

Com isso, vamos desenvolver um pouco mais

  lim h → 0 ⁡ sen ⁡ h h - cos ⁡ h h 2 =   lim h → 0 ⁡ h 2 2 ! - h 2 3 ! + h 4 5 ! - h 4 4 ! + h 6 6 ! - h 6 7 ! + … h 2 = lim h → 0 ⁡ h 2 1 2 ! - 1 3 ! + h 2 5 ! - h 2 4 ! + h 4 6 ! - h 4 7 ! + … h 2

Tendo um pouco mais de desenvolvimento

  lim h → 0 ⁡ sen ⁡ h h - cos ⁡ h h 2 = lim h → 0 ⁡ 1 2 ! - 1 3 ! + h 2 5 ! - h 2 4 ! + h 4 6 ! - h 4 7 ! + … = 1 2 ! - 1 3 ! + 0 - 0 + …

Com isso, temos o seguinte resultado

lim h → 0 ⁡ sen ⁡ h h - cos ⁡ h h 2 = 1 3

Passo 2

B – Pelo gráfico, temos o seguinte resultado

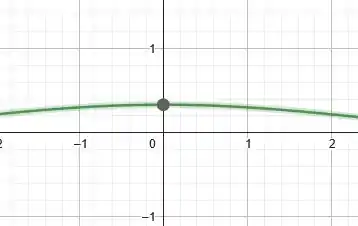
Resposta

Respondido acima!

Exercícios de Livros Relacionados

Utilize operações de séries de potências para encontrar a série de Taylor em x = 0 para as funções nos Exercícios 11-28. x 2 2 - 1 + cos ⁡ x
Utilize operações de séries de potências para encontrar a série de Taylor em x = 0 para as funções nos Exercícios 11-28. 2 1 - x 3
Utilize operações de séries de potências para encontrar a série de Taylor em x = 0 para as funções nos Exercícios 11-28. e x + 1 1 + x
Utilize operações de séries de potências para encontrar a série de Taylor em x = 0 para as funções nos Exercícios 11-28. x 2 cos ⁡ ( x 2 )
Utilize operações de séries de potências para encontrar a série de Taylor em x = 0 para as funções nos Exercícios 11-28. x e x