Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 10.Exercícios práticos - Ex. 74
Nos Exercícios 73-78:
a. Utilize séries de potências para avaliar o limite.
b. Em seguida, utilize um gráfico para provar seus cálculos
74.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
A – Podemos expandir esse limite da seguinte forma
Desenvolvendo os termos
Nós podemos fazer a substituição direta, nós temos que
Com isso, o limite será igual a
Passo 2
B – Pelo gráfico, nós temos que
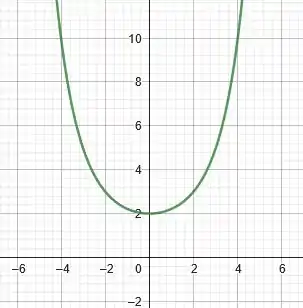
Podemos perceber que tende a .
Resposta
Exercícios de Livros Relacionados
Utilize operações de séries de potências para encontrar a série de Taylor em x = 0 para as funções nos Exercícios 11-28. 1 1 - x 2
Utilize operações de séries de potências para encontrar a série de Taylor em x = 0 para as funções nos Exercícios 11-28. cos 2 x (Sugestão: cos 2 x = ( 1 + cos 2 x ) / 2 . )
Utilize operações de séries de potências para encontrar a série de Taylor em x = 0 para as funções nos Exercícios 11-28. s e nx * cos x
Utilize operações de séries de potências para encontrar a série de Taylor em x = 0 para as funções nos Exercícios 11-28. x ln ( 1 + 2 x )
Utilize operações de séries de potências para encontrar a série de Taylor em x = 0 para as funções nos Exercícios 11-28. s e nx - x + x 3 3 !