Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 9.4 - Ex. 21
Existe evidência considerável para apoiar a teoria de que, para algumas espécies, existe uma população mínima de forma que as espécies se tornarão extintas se o tamanho da população cair abaixo de . Essa condição pode ser incorporada à equação logística pela introdução do fator . Então o modelo logístico modificado é dado pela equação diferencial
(a) Use a equação diferencial para mostrar que qualquer solução é crescente se e decrescente se .
(b) Para o caso onde , e , desenhe um campo de direções e use-o para esboçar várias curvas solução. Descreva o que acontece à população para várias populações iniciais. Quais são as soluções de equilíbrio?
(c) Resolva a equação diferencial explicitamente, usando frações parciais ou um sistema de computação algébrica. Use a população inicial .
(d) Use a solução na parte (c) para mostrar que se , então a espécie se tornará extinta. [Sugestão: Mostre que o numerador em sua expressão para é para algum valor de .]
Passo 1
(a) Hey, pessoal! Aqui a gente vai ter que lidar com essa nova equação diferencial, uma modificação da equação logística. Nós temos que mostrar para quais valores a solução é crescente ou decrescente. E como a gente faz isso?
Bom, basta olhar onde a derivada de é positiva ou negativa: se for positiva, é crescente; se for negativa, é decrescente. E olha que bom, já conhecemos a derivada de :
Agora temos que analisar o sinal de cada termo. Já sabemos que é uma constante positiva e que , a população, é sempre maior ou igual a , né?
Então, se os outros dois termos forem de sinais iguais, a derivada é positiva; e se forem de sinais diferentes, a derivada é negativa. Vamos olhar cada caso:
- Ambos positivos:
- Ambos negativos:
- O primeiro é positivo e o segundo é negativo:
- O primeiro é negativo e o segundo é positivo:
Mas é impossível , pois é tipo uma população máxima e é a mínima.
Pelo mesmo motivo já citado, se a população é menor que a mínima, então já é menor que a máxima, por isso já tem sentido suficiente afirmar que ela é menor que a mínima.
Novamente, se a população é maior do que a máxima, então já é maior que a mínima.
Assim, fica provado: a solução tem derivada positiva, e portanto é crescente, quando ; a solução tem derivada negativa, e portanto é decrescente, quando
Passo 2
(b) Com os dados do enunciado, a equação diferencial fica assim:
Agora vamos esboçar seu campo de direções com algumas curvas solução:
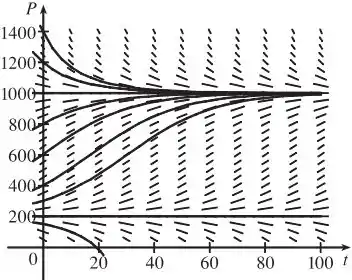
Quando a população começa abaixo de , ou seja, , ela tende a cair pra , o que é justamente o que se espera pois . Se , a solução cresce para Se , tende a decrescer para . E quando ou , elas são constantes, pois ambas são soluções de equilíbrio.
Passo 3
(c) Agora vamos resolver a equação diferencial usando um sistema de computação algébrica:
Passo 4
(d) Show! Vamos mostrar agora que, se , então a população está fadada a se extinguir.
Seguindo a sugestão, vamos olhar pro numerador da expressão que a gente encontrou pra e tentar igualar a Se a gente conseguir encontrar um valor de tal que isso aconteça, então provamos o que queríamos. Vamo lá?
Agora só precisamos provar que essa expressão é positiva.
Veja que a constante que multiplica o logaritmo é positiva, pois e , pois a população máxima é sempre maior do que a população mínima.
Então a gente tem que provar que o logaritmo é positivo. Mas quando isso acontece?
Como o logaritmo está na base , a expressão dentro do logaritmo também tem que ser maior do que pra ele ser positivo, beleza?
Se essa inequação se mostrar verdadeira, então provamos. Vamos multiplicar os dois lados por Mas lembre-se que esse termo é negativo (pois ), e portanto, o sinal inverte para , olha só:
É isso aí! A população mínima é sempre menor do que a “população máxima”, então tá provado!
Resposta
(c)