Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 5.3 - Ex. 1

Explique claramente o que você entende por “derivação e integração são processos inversos”.

Passo 1

Opa! Blz?

Aqui temos que explicar: derivação e integração são processos inversos.

Assim como nas operações mais básicas da matemática, saímos de um ponto com uma aplicação e voltemos nesse mesmo ponto quando aplicamos a operação inversa. Temos os exemplos de quando somamos uma quantidade a um número, e depois subtraímos uma mesma quantidade do número resultante temos como resultado o número inicial. Outro exemplo é pegarmos um número dividi-lo por certa quantia e logo após multiplicarmos pela mesma quantia voltando, assim, no número original. De modo análogo se integrarmos uma função e deriva-la em seguida voltamos a ter a mesma função.

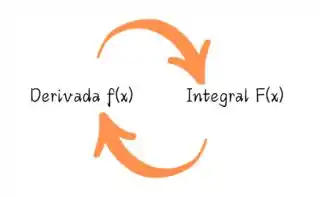
Passo 2

Por exemplo, considere uma função f x = x n + C (potencial)

  • Derivando f ( x ) , obtemos sua derivada f ' ( x ) da seguinte forma:

    • f ' x = n x n - 1

    Lembre-se que a derivada de uma constante é 0 .

    • A integral de uma função potencial:

    ∫ f ( x ) d x = x n + 1 n + 1 + C

  • Integrando f ' ( x ) , voltamos a f ( x ) , observe:

∫ f ' ( x ) d x = ∫ n x n - 1 d x

n ⋅ x n - 1 + 1 ( n - 1 ) + 1 + C

Simplificando:

n ⋅ x n n + C → x n + C

Viu que saímos na mesma função original?

Outra função que é fácil de ver isso é as trigonométricas, sen ⁡ x e cos ⁡ x , olha só essa imagem:

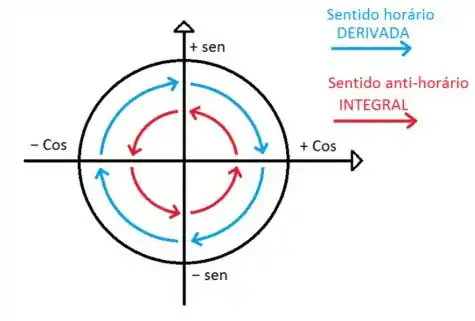
A relação inversa entre derivação e integração é capturada pelo Teorema Fundamental do Cálculo, que estabelece que se F ( x ) é uma primitiva de f ( x ) (ou seja, F ' ( x ) = f ( x ) ), então

Resumindo, derivação nos dá a inclinação da função em cada ponto, enquanto integração nos dá a área sob a curva da função em um intervalo. Eles são inversos porque a integração desfaz a derivada, e vice-versa.

Assim, a derivada nos diz como a função muda, enquanto a integral nos ajuda a encontrar a área sob a curva da função.

Resposta

Assim como nas operações mais básicas da matemática, saímos de um ponto com uma aplicação e voltemos nesse mesmo ponto quando aplicamos a operação inversa. Temos os exemplos de quando somamos uma quantidade a um número, e depois subtraímos uma mesma quantidade do número resultante temos como resultado o número inicial. Outro exemplo é pegarmos um número dividi-lo por certa quantia e logo após multiplicarmos pela mesma quantia voltando, assim, no número original. De modo análogo se integrarmos uma função e deriva-la em seguida voltamos a ter a mesma função.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a parte 1 do Teorema fundamental do Cálculo para encontrar a derivada da função y = ∫ 1 - 3 x 1 u 3 1 + u 2d u
Use a parte 1 do Teorema Fundamental do Cálculo para encontrar a derivada da função. g x = ∫ 1 x 1 t 3 + 1 d t
Esboce a área representada por g ( x ) . A seguir, encontre g ' ( x ) de duas maneiras: (a) utilizando a parte 1 do Teorema Fundamental e (b) calculando a integral usando a Parte 2 e então derivando.
Use a parte 1 do Teorema Fundamental do Cálculo para encontrar a derivada da função. g x = ∫ 1 x ln ⁡ td t
Use a parte 1 do Teorema Fundamental do Cálculo para encontrar a derivada da função. g u = ∫ 3 u 1 x + x 2 d x