Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.5 - Ex. 22
Explique por que a função é descontínua no dado número . Esboce o gráfico da função.
Passo 1
Olá, meu nobre amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
O enunciado fornece uma função e um ponto e pede para justificarmos o motivo de não ser contínua nesse ponto.
Relembrando, para uma função ser contínua em um ponto ela deve estar definida neste ponto e além disso, o valor da função neste ponto deve coincidir com o valor do limite. É isso que temos que verificar.
Passo 2
Vamos calcular o limite de quando tende a . Quando tomamos o limite, nos aproximamos de por valores de próximos de porém nunca iguais a . Então, a expressão que devemos usar para o limite é
Como , temos uma indeterminação do tipo 0/0:
Para eliminá-la, devemos fatorar o numerador.
Passo 3
Todo polinômio de segundo grau da forma com raízes reais pode ser fatorado na forma onde e são as raízes. Considerando o polinômio , suas raízes são obtidas pela fórmula de Bháskara:
e
Assim, temos que
Passo 4
Assim o limite fica
Simplificando o termo , o limite fica
Como , a função não é contínua em .
Passo 5
O esboço do gráfico da função está abaixo e foi feito no GeoGebra:
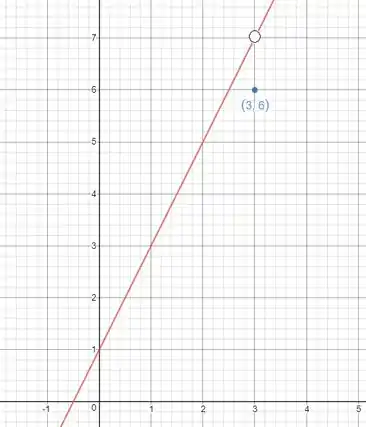
Resposta
R: demonstração e esboço de gráfico.