Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.5 - Ex. 19
Explique por que a função é descontínua no número dado, esboce o gráfico da função.
Passo 1
Opa, bora lá! O enunciado nos dá a função:
E pede pra a gente explicar porque ela é descontínua em .
Então primeiro de tudo, vamos relembrar que uma função é contínua num ponto, quando seu limite é igual ao seu valor naquele ponto:
No caso aqui, o nosso ponto de interesse é e já temos da própria função que:
Então o negócio é calcular o limite nesse ponto, bora?
Passo 2
Nessa função, se a gente substituir na primeira expressão, vamos achar uma indeterminação:
Ent��o vamos ter que dar um jeito de sumir com a indeterminação pra calcular esse limite. E a fatoração é sempre uma manipulação matemática que a gente tem que cogitar, porque frequentemente ela é a nossa saída.
Repara que o numerador pode ser fatorado. Por Bashkara, encontramos suas raízes:
As raízes do numerador são e , então sua forma fatorada fica:
Portanto:
AGORA PRESTA ATENÇÃO!
Toda vez que a gente vai cortar termos, a gente tem que checar se essa simplificação é válida, pois “cortar” termos iguais do numerador e do denominador significa dividir o numerador e o denominador por esse termo. Então pra que a gente possa fazer isso, é preciso que esse termo seja diferente de 0, pois não podemos fazer divisão por 0.
Pra função , não podemos cortar o , pois esse termo fica nulo quando . Mas que bom que na nossa função da questão isso não acontece:
Na nossa , quando , e não igual a .
Calma! Se isso foi confuso, tenta ler de novo com mais calma. Eu apenas estou explicando porque podemos cortar o , porque as vezes não podemos!
Mas bem, vamos lá. Simplificando, nossa função vai ficar:
Ufa conseguimos! Agora, no passo 3, vamos calcular o limite que a gente falou la no passo 1.
Passo 3
Bom, relembrando, a função no ponto vale:
Agora queremos calcular o limite quando pra ver se ele é igual à função nesse ponto:
Putz, são diferentes. Então se o limite da função num ponto é diferente do valor da função nesse ponto
Então a função é DESCONTÍNUA nesse ponto!
Passo 4
Por fim, vamos plotar o gráfico de:
é uma reta com inclinação e que cruza o eixo no ponto .
A única diferença dessa reta pra nossa função é o ponto em que .
Neste ponto, temos uma bolinha vazia na reta, pois
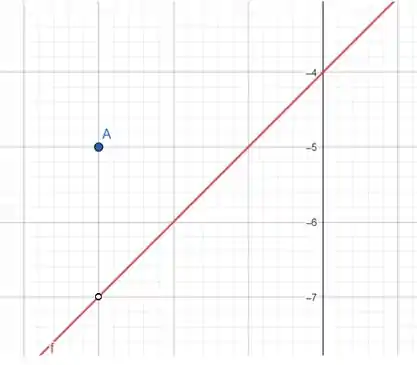
Prontinho!
Resposta
(a) A função é descontínua nesse ponto, pois
(b)
