Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.5 - Ex. 21
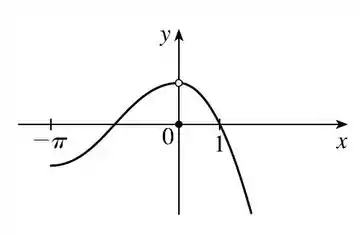
Explique porque a função é descontínua no número dado . Desenho o gráfico da função.
Passo 1
E aí, tudo bem? Nesse problema temos a seguinte função:
E já de cara o enunciado diz que a função não é contínua no ponto e a nossa missão aqui é dizer o motivo! Depois a gente vai desenhar essa função e isso vai nos mostrar visualmente que a função realmente não é contínua.
Só relembrando, uma função contínua é aquela que você consegue desenhar sem tirar o lápis do papel, mas aqui a gente vai usar a definição de limites laterais!
Se nos aproximamos pela direita e pela esquerda de um mesmo ponto, devemos chegar ao mesmo valor pra dizer que a nossa função é contínua. Em matemátiques temos:
Além disso precisamos que:
Olhando pra a nossa função vimos que temos um ponto de “colagem” em e é justamente esse ponto que vamos investigar!
Passo 2
Iremos calcular os limites laterais de . Começando pela esquerda, temos , então:
Temos que:
Então:
Agora pela direita, temos , então:
Os limites laterais são iguais! Porém temos:
O que é diferente dos limites laterais que a gente encontrou, portanto provamos que a nossa função não é contínua nesse ponto!
Passo 3
Agora vamos desenhar o gráfico. Lembrando da nossa função:
Podemos fazer uma tabelinha, pra :
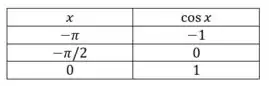
Não se assuste com o ali na tabelinha. A função não é essa nesse ponto mas ela tende a . Então podemos desenhar até pertinho, mas não no ponto em si. Agora pra
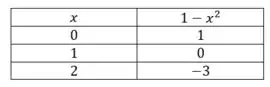
De novo, só colocamos o ponto pra prever o comportamento da função!
Juntando as informações e colocando no gráfico temos:
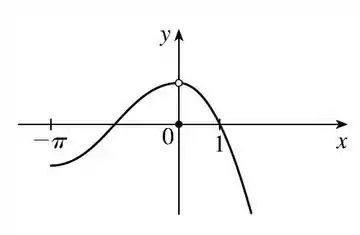
Como esperávamos, pra desenhar esse gráfico temos que “tirar o lápis do papel” quando chegamos em . Portanto a função não é contínua!
Resposta
Demonstração e:
