Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.5 - Ex. 22
Explique porque a função é descontínua no número dado . Desenho o gráfico da função.
Passo 1
Fala aí! tudo certinho?
Nesse problema foi dada uma função definida por partes
E nosso objetivo é explicar por que a função é descontinua em .
Tem ideia de como fazemos isso?
Para resolver esse problema, temos que verificar, por meio do limite de para tendendo a , qual o valor que a função tende a assumir quando se aproxima de .
Perceba que em a função é mas para a função ser contínua tem que tender a quando tende a .
Veja só!
Passo 2
Iremos calcular o limite da função no ponto
Se a gente substituir por , vamos cair em uma indeterminação . Nesses casos, como temos dois polinômios no numerador e no denominador podemos tentar simplificá-los por meio da fatoração de um deles.
Fatorando o numerador, chegamos em
Substituindo no limite...
Agora podemos simplificar o termo que aparece no numerador e no denominador, sendo assim:
E substituindo o valor de :
No entanto, conforme fornecido no enunciado, , dessa forma, é descontínua no ponto 3.
Show?
Passo 3
Podemos verificar o que foi posto no passo 2 através da análise do gráfico da função .
Esboçando na forma simplificada
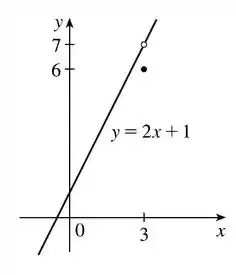
E aí! entendeu tudo? Responde Aí!