Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.2 - Ex. 56
Explique a relação entre continuidade e derivabilidade.
Passo 1
Se for diferenciável no ponto , então será contínua em .
Entretanto o contrário não é verdadeiro, se uma função for contínua em isso não implica que é diferenciável no ponto . Temos como exemplo a função:
Veja o gráfico da função abaixo:
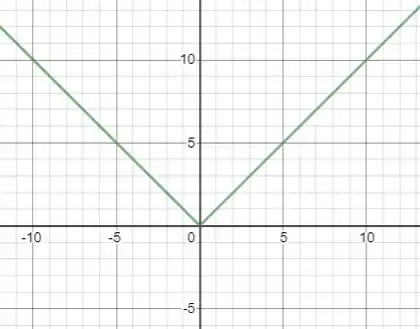
Ela é contínua em , pois existe , porém não é diferenciável nesse ponto, pois aí temos um bico, não podemos encontrar uma reta tangente nesse ponto.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
28. Dada f x = 1 - x 2 3 / 2 . (a) Prove que f é contínua no intervalo fechado - 1,1 . (b) Prove que f é derivável no intervalo aberto ( - 1,1 ) e que ambas f ´ + - 1ef ´ - ( 1 ) existem. (c) Faça um
33. Dada f x = x - 1 [ x ] . Faça um esboço do gráfico de f para x e [0,2]. Ache, se existirem: (a) f ´ - 1 ; (b) f ´ + 1 ; (c) f ´ 1 .
37. Na ilustração 1 temos a função valor absoluto definida por f x = x e essa função não é derivável em 0. Prove que f ´ x = x / x para todo x ≠ 0 . (Sugestão: seja x = x 2 .
40. Um fabricante pode obter um lucro de 20 dólares em cada item se até 800 itens forem produzidos por semana. O lucro decresce 0,02 dólares por item acima de 800. (a) Se x itens forem produzidos por
38. Se f x = x e g x = - x , (a) ache uma fórmula para f + g x . (b) Prove que f + g é derivável em 0, embora nem f nem g sejam deriváveis nesse númeroLetra (a)