Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 1.4 - Ex. 4d
Expresse o conjunto das soluções da inequação dada em notação de intervalo.
Passo 1
Vamos fatorar a expressão para ficar melhor de trabalhar, aqui vamos usar produtos notáveis:
Vamos lembrar desse produto notável:
Pronto, se encaixa direitinho na expressão, vamos aplicar então:
Agora vamos substituir na inequação:
Passo 2
Vamos agora analisar os sinais das expressões separadamente:
Para temos:
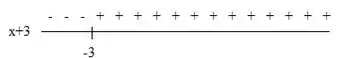
Aqui a expressão assume valores negativos quando e assume valores positivos quando .
Para temos:
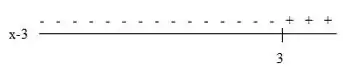
Aqui a expressão assume valores negativos quando e assume valores positivos quando .
Passo 3
Vamos analisar as duas imagens que achamos no passo anterior:
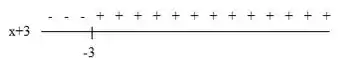
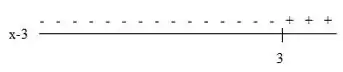
Temos que quando as duas expressões tiverem sinais opostos, analisando as duas imagens vemos que isso acontece quando:
Assim o conjunto solução é: