Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 14
Expresse D como a região do tipo I e também como uma região do tipo II. Em seguida, calcule a integral dupla de duas maneiras.
D é limitada pelas retas ,
Passo 1
Fala galera, tudo bem com vocês?
Nessa questão, temos uma região e precisamos expressar como região do tipo I e do tipo II, e calcular a integral dupla das duas maneiras.
D é limitada pelas retas , .
Vamos pensar juntos, ok?
Parar resolver, vamos lembrar de região tipo I e II.
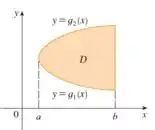
Uma região do tipo I é uma região limitada acima e abaixo por uma curva, além disso, é limitada lateralmente por retas verticais. A região e a integral têm essa cara:
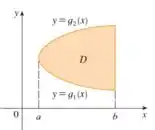
Já uma região do tipo II é o contrário. É uma região limitada lateralmente por curvas, mas acima e abaixo por retas horizontais. Logo, vamos ter:
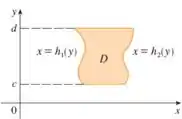
Sabendo disso, e só esboçar nossa região no formato tipo I e II. Lembrando que para escrever no formato do tipo II, e só escrevermos . Já os pontos de intersecção entre as curvas, basta igualarmos as expressões.
Agora ficou moleza ein! Vamos seguir esses passos e gabaritar essa!
Passo 2
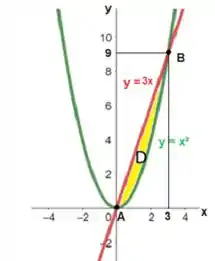
Primeiramente, vamos esboçar a nossa região. Portanto,
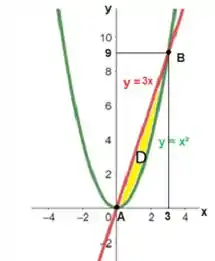
Em vermelho temos a reta:
Em verde temos a parábola:
Observe que nossa região é a que está em amarelo, entre essas duas curvas.
As duas curvas se intersectam nos pontos e . Para determinar esses pontos de intersecção, vamos igualar as funções:
Portanto, a intersecção entre as curvas ocorre no ponto e no ponto .
Passo 3
Agora podemos começar a escrever a nossa região.
Como a região do tipo I é limitada acima por uma curva e abaixo por outra:
Agora, avaliando nossa figura temos que:
Assim, podemos montar nossa integral como:
Passo 4
Nosso objetivo agora é resolver essa integral dupla definida na região tipo I.
Lembra que começamos a integrar de dentro para fora.
Integrando em , temos:
Aplicando os limites de integração:
Agora ficamos com uma integral simples em . Integrando, vamos ter:
Logo a integral na região tipo I é:
Passo 5
Já fizemos para a região do tipo I.
Agora, vamos escrever a nossa região como uma região do tipo II. Portanto, ela é limitada a esquerda por uma curva e a direita por outra curva.
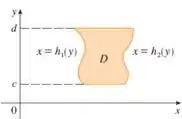
Lembre-se que precisamos escrever em função de , Avaliando nossa figura, temos que:
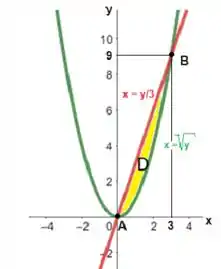
Acima ela é limitada pela reta (se resume a um ponto) e abaixo por outra reta . Observem que estas retas são dadas pelos pontos de interseção das curvas. Logo,
Portanto, a nossa integral fica:
Passo 6
Agora, vamos resolver a integral dupla do tipo II.
Lembre-se que sempre começamos a integrar de dentro para fora. Integrando em vamos ter:
Aplicando os limites de integração:
Agora ficamos com uma integral simples em . Integrando temos que:
Aplicando os limites de integração:
Logo a integral na região tipo II é:
Observe que obtemos as mesmas respostas na integral do tipo I e na integral do tipo II. Isso ocorre devido à continuidade da função e à aplicação do teorema de Fubini.
