Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 12b
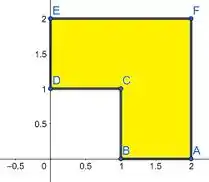
Desenhe um exemplo de uma região que seja
- Nem do tipo I nem do tipo II.
Passo 1
E aiiiii pessoal, tudo bem? Vamos começar!
Precisamos desenhar um exemplo de uma região. Para o item (b) fazer o desenho de uma região que não é do tipo I e II.
Muita calma agora, beleza! Vamos utilizar softwares para plotar as regiões.
Mas antes, precisamos saber o que é região do tipo I e uma do tipo II?
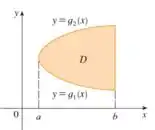
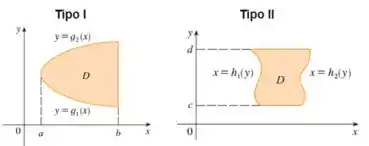
A região do tipo I é uma região limitada acima e abaixo por uma curva, além disso, é limitada lateralmente por retas verticais. Portanto, o seu domínio tem essa cara:
Escrevemos a integral do tipo 1 da seguinte forma:
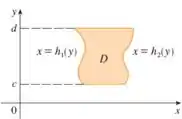
Para uma região do tipo II é o contrário. É uma região limitada lateralmente por curvas, mas acima e abaixo por retas horizontais. Portanto, temos o seguinte domínio:
A integral do tipo 2, é escrita como:
Como queremos fazer uma região que não é do tipo I e II, precisamos fazer uma figura que não vai seguir os critérios mencionados acima.
Agora ficou fácil ein! Bora lá começar!
Passo 2
Preste bem atenção na figura a seguir. Vamos escolher uma região limitada pelos pontos , , , , e .
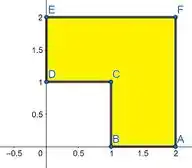
Agora vamos comparar a região tipo I e II com a nossa figura:
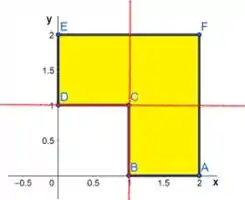
Para ser do tipo I, deveríamos ter apenas duas curvas escritas em . Observe em relação ao eixo , que vamos ter três retas. São elas:
Já para o tipo II, deveríamos ter apenas duas curvas escritas em . Observe em relação ao eixo , que vamos ter três retas. São elas:
Porque escolhemos essa região?
Por que não conseguimos escrever como região do tipo I e II. Pois vamos ter mais de duas expressões. Nesse caso vamos precisar usar um outro teorema, onde dividimos em duas regiões e .
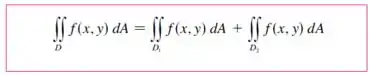
Resposta
